
2.(2010海南省高考调研卷)
已知椭圆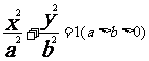 的长轴长为
的长轴长为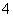 ,离心率为
,离心率为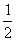 ,
,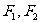 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点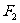 ,且与直线
,且与直线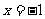 相切。
相切。
(Ⅰ) (ⅰ)求椭圆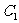 的方程;
的方程;
(ⅱ)求动圆圆心轨迹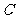 的方程;
的方程;
(Ⅱ) 在曲线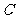 上有两点
上有两点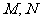 ,椭圆
,椭圆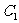 上有两点
上有两点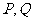 ,满足
,满足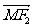 与
与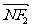 共线,
共线,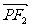 与
与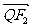 共线,且
共线,且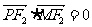 ,求四边形
,求四边形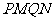 面积的最小值。
面积的最小值。
1.(2010东北师大附中最后模拟)
已知圆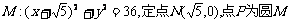 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足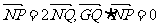 .
.
(I)求点G的轨迹C的方程;
(II)过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设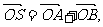 是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
12. 解:(Ⅰ)假设∥,则2cosx(cosx+sinx)-sinx(cosx-sinx)=0,
∴2cos2x+sinxcosx+sin2x=0,2·+sin2x+=0,即sin2x+cos2x=-3,
∴(sin2x+)=-3,与|(sin2x+)|≤矛盾,故向量与向量不可能平行.
(Ⅱ)∵f(x)=·=(cosx+sinx)·(cosx-sinx)+sinx·2cosx=cos2x-sin2x+2sinxcosx=cos2x+sin2x=(cos2x+sin2x)=(sin2x+),
∵-≤x≤,∴-≤2x+≤,∴当2x+=,即x=时,f(x)有最大值;
当2x+=-,即x=-时,f(x)有最小值-1.
11. 解:(I)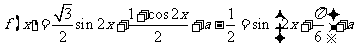 ,
,
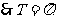 ……………3分
……………3分
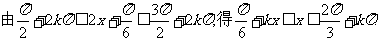
故函数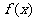 的单调递减区间是
的单调递减区间是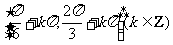 .
………6分
.
………6分
(II)
当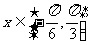 时,原函数的最大值与最小值的和
时,原函数的最大值与最小值的和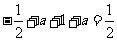 ,
,
解得a=0 . ………8分
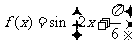 ,图象如图. ………………12分
,图象如图. ………………12分

10. 解:(1)由题意知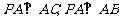 ,则
,则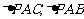 均为直角三角形…………………1分
均为直角三角形…………………1分
在 中,
中,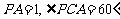 ,解得
,解得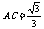 …………………………2分
…………………………2分
在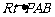 中,
中,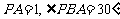 ,解得
,解得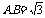 …………………………3分
…………………………3分
又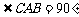 ,
,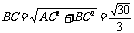 万米. …………………………5分
万米. …………………………5分
(2)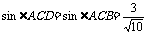 ,
,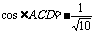 ,…………………………7分
,…………………………7分
又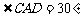 ,所以
,所以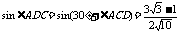 .…………………………9分
.…………………………9分
在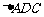 中,由正弦定理,
中,由正弦定理,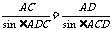 …………………………10分
…………………………10分
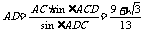 万米…………………………12分
万米…………………………12分
9. 根据余弦定理 AB2=a2+b2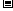 2abcos
2abcos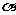 , AB=
, AB= .……………4分
.……………4分
cosB=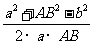 =
=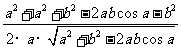
=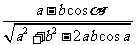 ,从而确定
,从而确定 B的大小. ……………8分
B的大小. ……………8分
同理可以得到cosA=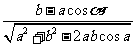 ,从而确定
,从而确定 A的大小. …………12分
A的大小. …………12分
8. (1)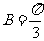 ,(2)
,(2)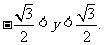
7. 由题意知: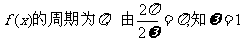 。------------3分
。------------3分
由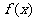 最大值为2,故
最大值为2,故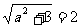 ,又
,又 ,
,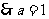 ------------6分
------------6分
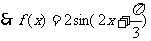 ……………………………………… 7分
……………………………………… 7分
(II)由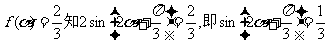 。
。
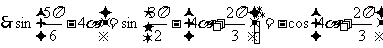
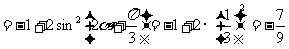 。………………………12分
。………………………12分
6. 解:(Ⅰ)(方法一)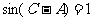 ,又
,又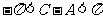 ,
,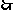
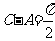 , ……..1分
, ……..1分
又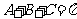 ,∴
,∴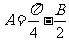 ,
……………………..2分
,
……………………..2分
∴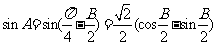 ,
……………………..4分
,
……………………..4分
∴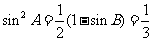 ,又
,又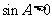 ,∴
,∴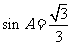 . ……………………6分
. ……………………6分
(方法二)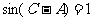 ,又
,又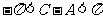 ,
,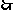
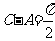 , ………1分
, ………1分
又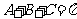 ,∴
,∴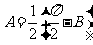 ,
……………………..2分
,
……………………..2分
∴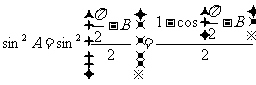 ,
……………………..4分
,
……………………..4分
∴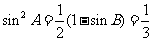 ,又
,又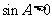 ,∴
,∴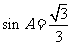 . ……………………6分
. ……………………6分
又(方法三)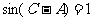 ,又
,又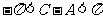 ,
,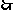
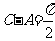 , ……..1分
, ……..1分
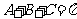 ,∴B=
,∴B=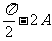 ,
……………………2分
,
……………………2分
∵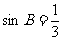 ∴
∴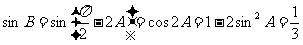 ,
,
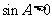 ,∴
,∴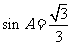 . ……………………6分
. ……………………6分
(Ⅱ)由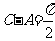 易知
易知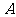 、
、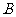 都是锐角,
都是锐角,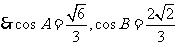 ,
,
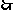
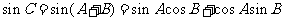
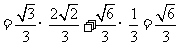 ,…8分
,…8分
由正弦定理可知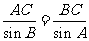 ∴
∴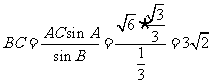 ,
……10分
,
……10分
∴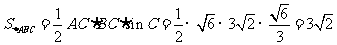 . ……………….12分
. ……………….12分
5. ⑴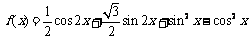
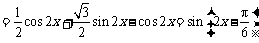 ,
,
∴最小正周期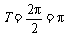 .
.
由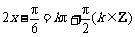 ,得
,得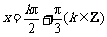
函数图象的对称轴方程为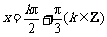
⑵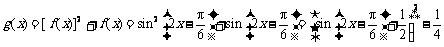
当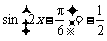 时,
时,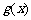 取得最小值
取得最小值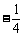 ;
;
当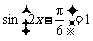 时,
时,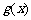 取得最大值2,
取得最大值2,
所以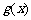 的值域为
的值域为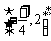 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com