
6.(陕西长安二中2008届高三第一学期第二次月考)已知函数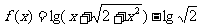
(1)判断函数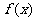 的奇偶性。 (2)判断函数
的奇偶性。 (2)判断函数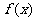 的单调性。
的单调性。
解 (1)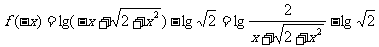
=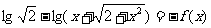
∴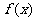 为奇函数
为奇函数
(2)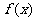 是R上的增函数,(证明略)
是R上的增函数,(证明略)
5.(江苏省南通市2008届高三第二次调研考试)幂函数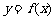 的图象经过点
的图象经过点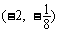 ,则
,则
满足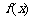 =27的x的值是
.
=27的x的值是
.
答案
4.(2008年高考数学各校月考试题)已知函数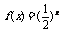 的图象与函数g(x)的图象关于直线
的图象与函数g(x)的图象关于直线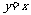 对称,令
对称,令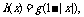 则关于函数
则关于函数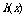 有下列命题:
有下列命题:
①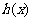 的图象关于原点对称; ②
的图象关于原点对称; ②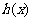 为偶函数;
为偶函数;
③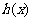 的最小值为0; ④
的最小值为0; ④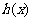 在(0,1)上为减函数.
在(0,1)上为减函数.
其中正确命题的序号为 (注:将所有正确命题的序号都填上)
答案 ②③
3.(2007届高三数学二轮复习新型题专题训练)一次研究性课堂上,老师给出函数
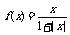 (x
(x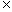 R),三位同学甲、乙、丙在研究此函数时分别给出命题:
R),三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数f(x)的值域为(-1,1);乙:若x1≠x2,则一定有f(x1)≠f(x2);
丙:若规定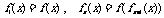 ,
,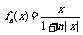 对任意
对任意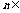 N*恒成立.
N*恒成立.
你认为上述三个命题中正确的个数有 ( )
A.0个 B.1个 C.2个 D.3个
答案 D
2.(2007届岳阳市一中高三数学能力题训练)已知a>1,则函数f(x)= loga x的图象与其反函数y=f-1(x)的图象 ( )
A.不可能有公共点 B.不可能只有一个公共点
C. 最多只有一个公共点 D.最多只有两个公共点
答案 D
1.(2008年高考数学各校月考试题)若lga+lgb=0(其中a≠1,b≠1),则函数f(x)=ax与g(x)=bx的图象 ( )
A.关于直线y=x对称 B.关于x轴对称
C.关于y轴对称 D.关于原点对称
答案 C
解析 取满足 可得答案C.
可得答案C.
14.(2009广东三校一模)设函数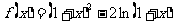 .
.
(1)求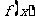 的单调区间;
的单调区间;
(2)若当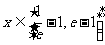 时,(其中
时,(其中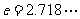 )不等式
)不等式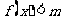 恒成立,求实数
恒成立,求实数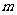 的取值范围;
的取值范围;
(3)试讨论关于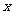 的方程:
的方程: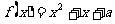 在区间
在区间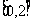 上的根的个数.
上的根的个数.
解
(1)函数的定义域为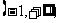
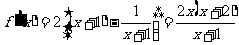 . 1分
. 1分
由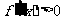 得
得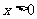 ; 2分
; 2分
由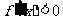 得
得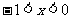 ,
3分
,
3分
则增区间为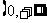 ,减区间为
,减区间为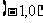 . 4分
. 4分
(2)令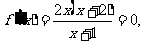 得
得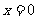 ,由(1)知
,由(1)知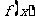 在
在 上递减,在
上递减,在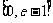 上递增, 6分
上递增, 6分
由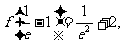
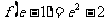 ,且
,且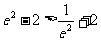 ,
8分
,
8分
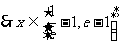 时,
时,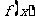 的最大值为
的最大值为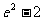 ,故
,故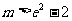 时,不等式
时,不等式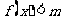 恒成立. 9分
恒成立. 9分
(3)方程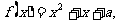 即
即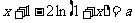 .记
.记 ,则
,则
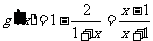 .由
.由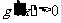 得
得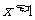 ;由
;由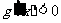 得
得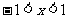 .
.
所以g(x)在[0,1]上递减,在[1,2]上递增.
而g(0)=1,g(1)=2-2ln2,g(2)=3-2ln3,∴g(0)>g(2)>g(1) 10分
所以,当a>1时,方程无解;
当3-2ln3<a≤1时,方程有一个解,
当2-2ln2<a≤a≤3-2ln3时,方程有两个解;
当a=2-2ln2时,方程有一个解;
当a<2-2ln2时,方程无解. 13分
字上所述,a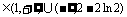 时,方程无解;
时,方程无解;
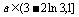 或a=2-2ln2时,方程有唯一解;
或a=2-2ln2时,方程有唯一解;
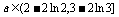 时,方程有两个不等的解. 14分
时,方程有两个不等的解. 14分
2007-2008年联考题
10.(江西师大附中2009届高三数学上学期期中)
已知定义域为R的函数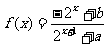 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的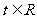 ,不等式
,不等式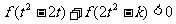 恒成立,求k的取值范围.
恒成立,求k的取值范围.
解 (1) 因为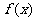 是R上的奇函数,所以
是R上的奇函数,所以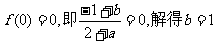
从而有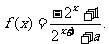 又由
又由 ,解得
,解得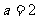
(2)解法一:由(1)知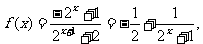
由上式易知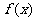 在R上为减函数,又因
在R上为减函数,又因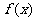 是奇函数,从而不等式
是奇函数,从而不等式
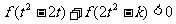 等价于
等价于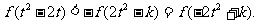
因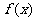 是R上的减函数,由上式推得
是R上的减函数,由上式推得
即对一切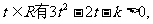 从而
从而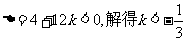
解法二:由(1)知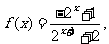
又由题设条件得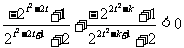
即
整理得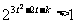 ,因底数2>1,故
,因底数2>1,故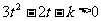
上式对一切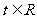 均成立,从而判别式
均成立,从而判别式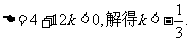
9.(江西南昌新民外语学校09届高三第一次月考)函数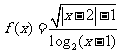 的定义域
的定义域
为 .
答案 
8.(2009中学第六次月考)定义区间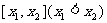 的长度为
的长度为 ,已知函数
,已知函数
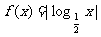 的定义域为
的定义域为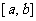 ,值域为
,值域为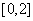 ,则区间
,则区间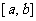 的长度的最大值与最小值的差为
.
的长度的最大值与最小值的差为
.
答案 3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com