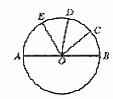
5. 如图，AB是直径，BC(︵)＝CD(︵)＝DE(︵)，∠BOC＝40°，

∠AOE的度数是　　 。

4. 在⊙O中，弦AB的长恰好等于半径，弦AB所对的圆心角为　　　　

3. ⊙O中，直径AB∥CD弦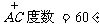，，则∠BOD=______。

1．如图,在⊙O中,　　　 　　　,

∠1=30°,则∠2=__________

2

圆心角为________。

2．运用圆心角、弧、弦之间的关系解决有关问题.

[课后作业]

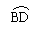
班级　　 姓名　　　　　 学号　　　

1．探索圆的中心对称性及有关性质的过程.

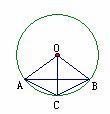例1．如图,AB、AC、BC都是⊙O的弦，∠AOC=∠BOC.∠ABC与∠BAC相等吗？为什么？

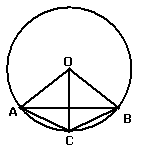例2.如图，AB、AC、BC都是⊙O的弦，∠AOC=∠BOC∠ABC与∠BAC相等吗？为什么？

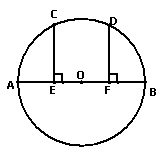
例3.已知：如图，AB是⊙O的直径，点C、D在⊙O上，CE⊥AB于E，DF⊥AB于F，且AE=BF，AC与BD相等吗？为什么？

3.总结

上面的命题反映了在同圆或等圆中，圆心角、弧、弦的关系，对于这三个量之间的关系，你还有什么思考？请与小组同学交流.

你能够用文字语言把你的发现表达出来吗?

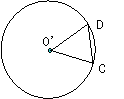　　 (1)在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等，那么　　　　　　　　　　　　　　 .

试一试：

如图,已知⊙O、⊙O半径相等，AB、CD

分别是⊙O、⊙O的两条弦.填空：

①若AB=CD，则　　　　　　　　　　　　 ，　　　　　　　　　

②若AB= CD，则　　　　　　　　　　 ，　　　　　　　　　

③若∠AOB=∠COD，则　　　　　 　　　，　　　 　　　　　　　.

思考：在圆心角、弧、弦这三个量中，角的大小可以用度数刻画，弦的大小可以用长度刻画，那么如何来刻画弧的大小呢？

(2)圆心角的度数与　　　　　　　 相等.

2.交流

在操作的过程中，你有什么发现，请与小组同学交流.

_______________________________________________

1.尝试

(1)在两张透明纸片上，分别作半径相等的⊙O和⊙O

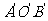(2)在⊙O和⊙O中,分别作相等的圆心角∠AOB、∠，连接AB、.

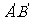(3)将两张纸片叠在一起，使⊙O与⊙O重合(如图).

(4)固定圆心，将其中一个圆旋转某个角度，使得OA与OA重合.