
24.解:(1)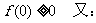
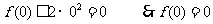
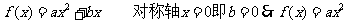
又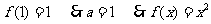
(2)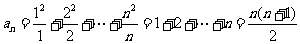
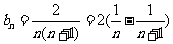
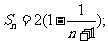
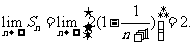
(3)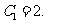
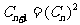
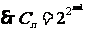
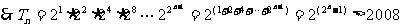
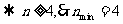
22.解:(1)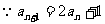 ,
,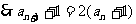 ……………………2分
……………………2分
故数列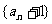 是首项为2,公比为2的等比数列。……………………3分
是首项为2,公比为2的等比数列。……………………3分
 ,
,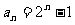 …………………………………………4分
…………………………………………4分
(2)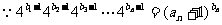 ,
,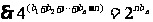 ……………5分
……………5分
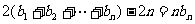 ①
①
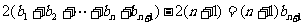 ②
②
②-①得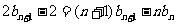 ,即
,即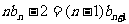 ③……………………8分
③……………………8分
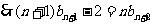 ④
④
④-③得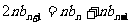 ,即
,即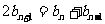 ……………………9分
……………………9分
所以数列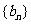 是等差数列
是等差数列
(3)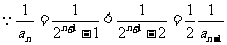 ………………………………11分
………………………………11分
设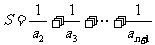 ,则
,则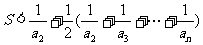
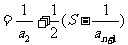
…………13分
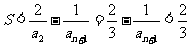 ………………………………14分
………………………………14分
15.解:(I)设 图象的两个交点
图象的两个交点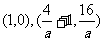
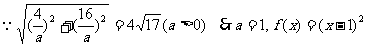
(II)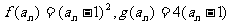

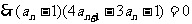 …………6分
…………6分

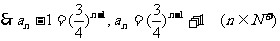 …………8分
…………8分
(III)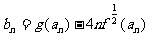
9.解:(1)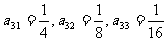 ……………………………………………………3分
……………………………………………………3分
(2)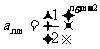 ……………………………………………………7分
……………………………………………………7分
(3)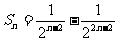
当 时,
时,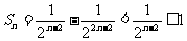 ,所以
,所以
当 时,
时,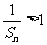 ,则
,则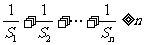
又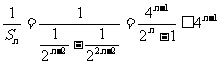
所以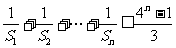 ………………………………………………12分
………………………………………………12分
7.解:(1)由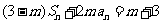 ,得
,得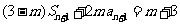 ,两式相减,得
,两式相减,得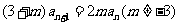 ,∴
,∴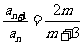 ,∵
,∵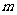 是常数,且
是常数,且 ,
,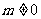 ,故
,故
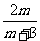 为不为0的常数,∴
为不为0的常数,∴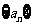 是等比数列。
是等比数列。
(2)由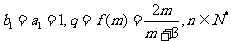 ,且
,且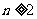 时,
时,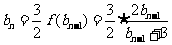 ,得
,得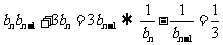 ,∴
,∴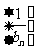 是以1为首项,
是以1为首项,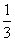 为公差的等差数列,
为公差的等差数列,
∴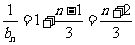 ,故
,故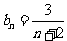 。
。
(3)由已知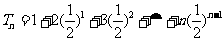 ,∴
,∴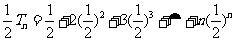
相减得: ,∴
,∴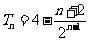 ,
,
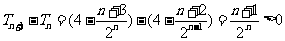 ,
,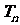 递增,∴
递增,∴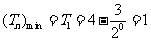 ,
,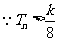 对
对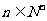 均成立,∴
均成立,∴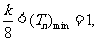 ∴,又
∴,又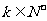 ,∴
,∴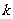 最大值为7。
最大值为7。
6. 
得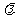 =2或
=2或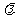 =-3 …………………………2分
=-3 …………………………2分
当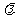 =2时,可得
=2时,可得 为首项是
为首项是 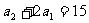 ,公比为3的等比数列,
,公比为3的等比数列,
则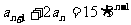 ①
①
当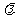 =-3时,
=-3时,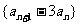 为首项是
为首项是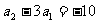 ,公比为-2的等比数列,
,公比为-2的等比数列,
∴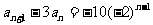 ②
②
①-②得,
 ………………4分
………………4分
(注:也可由①利用待定系数或同除2n+1得通项公式)
(Ⅱ)当k为奇数时,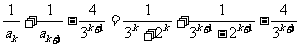
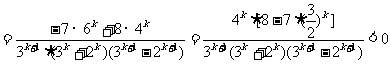
∴
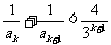 ……………………8分
……………………8分
(Ⅲ)由(Ⅱ)知k为奇数时, 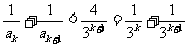 …………10分
…………10分
①当n为偶数时, 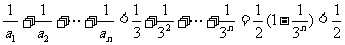
②当n为奇数时,
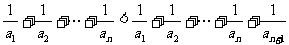
=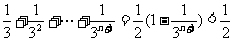 ………………13分
………………13分
5.解:(1)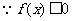 的解集有且只有一个元素
的解集有且只有一个元素
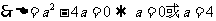
又由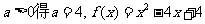
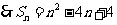
当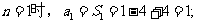
当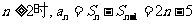
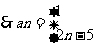
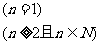 …………………………………(文6分,理5分)
…………………………………(文6分,理5分)
(2)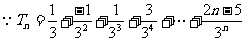 ①
①
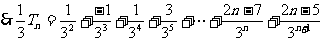 ②
②
由①-②得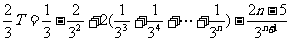
 …………………………………………(文13分,理10分)
…………………………………………(文13分,理10分)
(3)(理科)由题设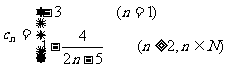
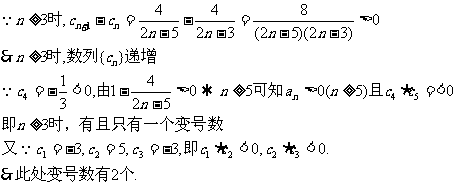
综上,得数列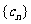 共有3个变号数,即变号数为3.……………………(理13分)
共有3个变号数,即变号数为3.……………………(理13分)
1.解:(Ⅰ)当n≥2时,2an=3Sn-4+2-Sn,即2(Sn-Sn-1)=3Sn-4+2-Sn,
所以Sn= Sn-1+2∴(n≥2)
又2+a2=×2+2=3 Þ a2=1 Þ ∴数列{an}是首项为2,公比为的等比数列
∴an=22-n(n∈N*)
(Ⅱ)由(Ⅰ)知an=22-n(n∈N*)则Tn=b1+b2+……+bn
=2×2+3×1+4×+……+(n+1)×22-n
∴ Tn= 2×1+3×+……+n×23-n+(n+1)×22-n,
作差得: Tn=2×2+1+++……+23-n-(n+1)22-n
=6- ∴Tn=12-(n∈N*)
(Ⅲ)证明: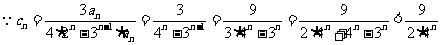

3解:(I)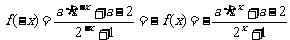 得
得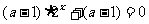
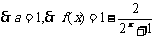 (2分)
(2分)
设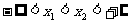
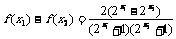

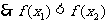
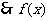 在R上单调递增
(4分)
在R上单调递增
(4分)
(Ⅱ)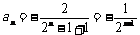 (5分)
(5分)
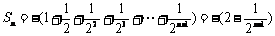 (7分)
(7分)
(III)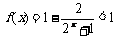
又f(x)为奇函数,且在R上为单调增函数
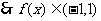 (9分)
(9分)
当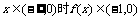
欲使 上有解
上有解
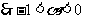 (10分)∴f(-1)<f(α)<f(0)
(10分)∴f(-1)<f(α)<f(0) 即
即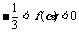
4.解:(Ⅰ)由
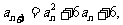 得
得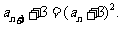
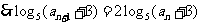 ,即
,即 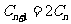 ,
,
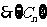 是以2为公比的等比数列 …………4分
是以2为公比的等比数列 …………4分
(Ⅱ) 又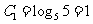
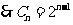 即
即 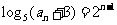 ,
,
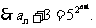 故
故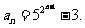
(Ⅲ)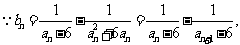 =
=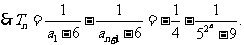
又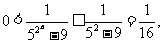
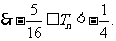
48、(江苏省常州市2008-2009高三第一学期期中统一测试数学试题)已知数列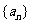 的首项
的首项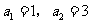 ,前
,前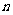 项和为
项和为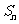 ,且
,且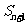 、
、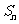 、
、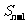 (n ≥2)分
(n ≥2)分
别是直线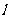 上的点A、B、C的横坐标,
上的点A、B、C的横坐标,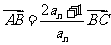 ,设
,设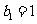 ,
,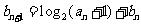 .
.
⑴ 判断数列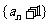 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
⑵ 设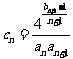 ,证明:
,证明: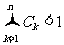 .
.
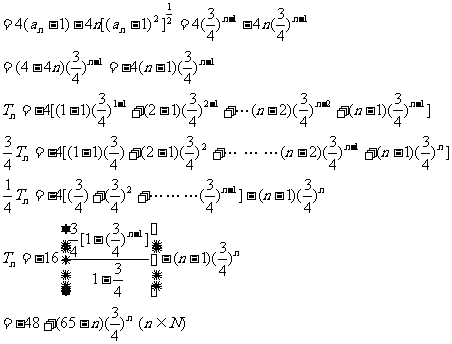
41、(2009届福建省福鼎一中高三数学强化训练综合卷一)已知数集序列{1}, {3, 5}, {7, 9,11}, {13, 15, 17, 19},……,其中第n个集合有n个元素,每一个集合都由连续正奇数组成,并且每一个集合中的最大数与后一个集合最小数是连续奇数,
(Ⅰ) 求第n个集合中最小数an的表达式;
(Ⅱ)求第n个集合中各数之和Sn的表达式;
(Ⅲ)令f(n)=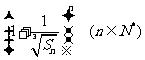 ,求证:2≤
,求证:2≤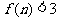
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com