
7.设函数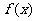 是定义在R上的奇函数,若当
是定义在R上的奇函数,若当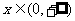 时,
时,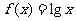 ,则满足
,则满足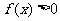 的
的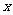 的取值范围是 ( )
的取值范围是 ( )
A.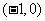 B.(1,+∞)
B.(1,+∞)
C.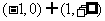 D.(
D.( -1,+∞)
-1,+∞)
6.某地西红柿2月1日开始上市,通过市场调查,得到西红柿的种植成本Q(单位:元 /100kg)与上市时间
/100kg)与上市时间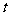 (单位:天)的数据如下表:
(单位:天)的数据如下表:
时间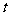 |
50 |
110 |
250 |
|
种植成本Q |
150 |
108 |
150 |
根据表中数据,下列函数模型中可以描述西红柿的种植成本Q与上市时间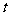 的变化关系的是 ( )
的变化关系的是 ( )
A.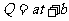 B.
B.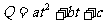
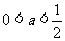
C.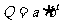 D.
D.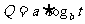
5.若命题“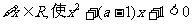 ”是假命题,则实数
”是假命题,则实数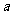 的取值范围为 (
的取值范围为 (
 )
)
A.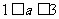 B.
B. C.
C.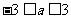 D.
D.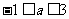
4.已知圆的极坐标方程为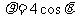 ,则圆心到直线
,则圆心到直线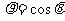 =3的距离是 ( )
=3的距离是 ( )
A.1 B.2 C.3 D.4
3.若方程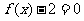 在(-∞,0)内有解,则
在(-∞,0)内有解,则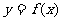 的图象是 ( )
的图象是 ( )

2.化简: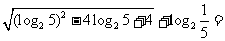 (
(  )
)
A.2 B.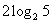 C.-2 D.
C.-2 D.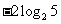
1.若集合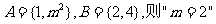 是
是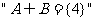 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不 必要条件
必要条件
21.(本小题满分13分)
已知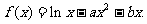
(1)若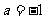 ,函数
,函数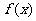 在其定义域内是增函数,求
在其定义域内是增函数,求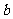 的取值范围;
的取值范围;
(2)当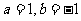 时,证明:函数
时,证明:函数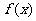 只有一个零点;
只有一个零点;
(3)若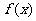 的图象与
的图象与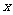 轴交于
轴交于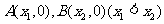 两
两 点,AB
点,AB 中点为
中点为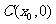 ,求证:
,求证: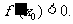
20.(本小题满分13分)
旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售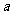 件。通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件。通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为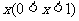 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为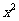 。记改进工艺后,旅游部门销售该纪念品的月平均利润是
。记改进工艺后,旅游部门销售该纪念品的月平均利润是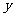 (元)。
(元)。
(1)写出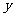 与
与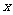 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大。
19.(本小题满分13分)
已知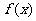 是二次函数,不等式
是二次函数,不等式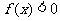 的解集是(0,5),且
的解集是(0,5),且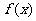 在区间[-1,4]上的最大值是12。
在区间[-1,4]上的最大值是12。
(1)求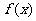 的解析式;
的解析式;
 (2)是否存在自然数
(2)是否存在自然数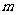 ,使得方程
,使得方程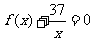 在区间
在区间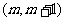 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出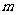 的
的 取值范围;若不存在,说明理由。
取值范围;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com