
6.一组数据中每个数据都减去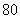 构成一组新数据,则这组新数据的平均数是
构成一组新数据,则这组新数据的平均数是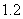 ,方差是
,方差是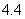 ,则原来一组数的方差为
,则原来一组数的方差为
5. 已知向量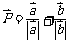 ,其中
,其中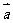 、
、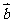 均为非零向量,则
均为非零向量,则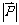 的取值范围是 .
的取值范围是 .
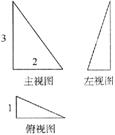
4. 一个空间几何体的主视图、左视图、俯视图为直角三角形,边长如图所示,那么这个几何体的体积为 .
3. 化简(cos225 º +isin225º)2(其中i为虚数单位)的结果为 .
2.命题“存在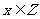 ,使
,使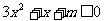 ”的否定是
。
”的否定是
。
1. 集合
集合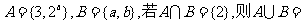
20.设A(x1,y1),B(x2,y2)是函数f(x)=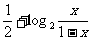 的图象上任意两点,且
的图象上任意两点,且
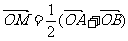 ,已知点M的横坐标为
,已知点M的横坐标为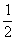 .
.
(1)求证:M点的纵坐标为定值;
(2)若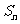 =
=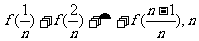 ∈N*,且n≥2,求
∈N*,且n≥2,求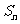 .
.
(3)已知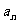 =
= 其中n∈N*.Tn为数列{an}的前n项和,
其中n∈N*.Tn为数列{an}的前n项和,
若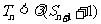 对一切n∈N*都成立,试求
对一切n∈N*都成立,试求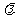 的取值范围.
的取值范围.
[解析](1)证明:∵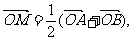 ∴M是AB的中点.设M点的坐标为(x,y),
∴M是AB的中点.设M点的坐标为(x,y),
由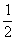 (x1+x2)=x=
(x1+x2)=x=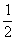 ,得x1+x2=1,则x1=1-x2或x2=1-x1.
,得x1+x2=1,则x1=1-x2或x2=1-x1.
而y=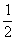 (y1+y2)=
(y1+y2)= 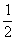 [f(x1)+f(x2)] =
[f(x1)+f(x2)] =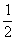 (
(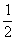 +log2
+log2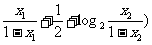
=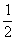 (1+log2
(1+log2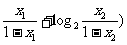 =
=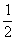 (1+log2
(1+log2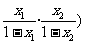
=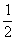 (1+log2
(1+log2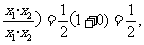 ∴M点的纵坐标为定值
∴M点的纵坐标为定值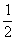 .
.
(2)由(1),知x1+x2=1,f(x1)+f(x2)=y1+y2=1,
Sn=f( Sn=f(
Sn=f(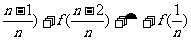 ,
,
两式相加,得
2Sn=[f(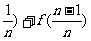 )+[f(
)+[f(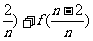 )+…+[f(
)+…+[f(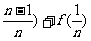 )
)
=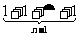 ,∴Sn=
,∴Sn=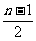 (n≥2,n∈N*).
(n≥2,n∈N*).
(3)当n≥2时,an=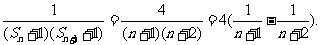
Tn=a1+a2+a3+…+an=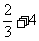 [(
[(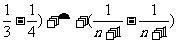 ]
]
=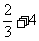 (
(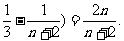
由Tn<λ(Sn+1+1),得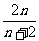 <λ·
<λ·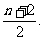 ∴λ>
∴λ>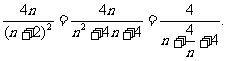
∵n+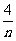 ≥4,当且仅当n=2时等号成立,∴
≥4,当且仅当n=2时等号成立,∴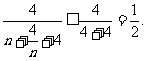
因此λ>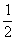 ,即λ的取值范围是(
,即λ的取值范围是(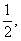 +∞).
+∞).
19.已知椭圆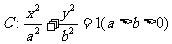 ,直线
,直线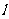 为圆
为圆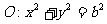 一条切线,记椭圆的离心率为
一条切线,记椭圆的离心率为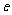 .
.
(Ⅰ)若直线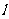 的倾斜角为
的倾斜角为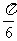 ,且恰好经过椭圆的右焦点,求
,且恰好经过椭圆的右焦点,求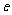 的大小;
的大小; 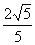
(Ⅱ)是否存在这样的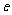 ,使得 (ⅰ) 椭圆的右焦点在直线
,使得 (ⅰ) 椭圆的右焦点在直线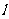 上;(ⅱ)原点
上;(ⅱ)原点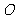 关于直线
关于直线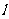 的对称点恰好在椭圆
的对称点恰好在椭圆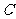 上同时成立.若存在,请求出
上同时成立.若存在,请求出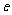 的大小;若不存在,请说明理由.
的大小;若不存在,请说明理由.
不存在
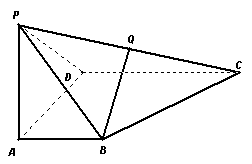
18. 如图,四边形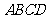 是直角梯形,
是直角梯形,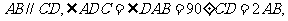
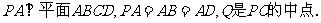
(Ⅰ) 求证: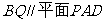 ;
;
(Ⅱ)
探究在过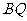 且与底面
且与底面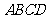 相交的平面中是否存在一个平面
相交的平面中是否存在一个平面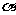 ,把四棱锥P-ABCD截成两部分,使得其中一部分为一个四个面都是直角三角形的四面体.若存在,求平面
,把四棱锥P-ABCD截成两部分,使得其中一部分为一个四个面都是直角三角形的四面体.若存在,求平面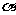 将四棱锥P-ABCD截成两部分的体积之比;若不存在,请说明理由.
将四棱锥P-ABCD截成两部分的体积之比;若不存在,请说明理由.
(Ⅱ)设过BQ的平面与平面PCD交于QE, E为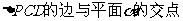 ,
,
当E为CD中点时,四面体Q-BCE的四个面都是直角三角形,证明如下:因为当E 为CD的中点时,则DE//AB且DE=AB,所以四边形ABED为平行四边形
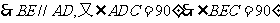 ,故
,故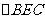 为直角三角形
为直角三角形
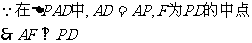
又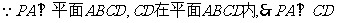 ,又
,又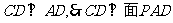
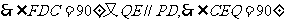 ,
,
又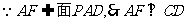 ,又
,又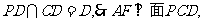
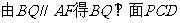
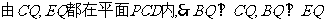 ,所以四面体Q-BCE的四个面都为直角三角形。此时体积之比为1:5
,所以四面体Q-BCE的四个面都为直角三角形。此时体积之比为1:5
17.已知函数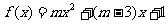 的图象与x轴的交点至少有一个在原点右侧.
的图象与x轴的交点至少有一个在原点右侧.
(1)求实数m的取值范围;
(2)令t=-m+2,求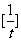 的值(其中[t]表示不大于t的最大整数).
的值(其中[t]表示不大于t的最大整数).
[解析]若m=0 则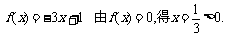 符合题意.
符合题意.
若m≠0 ,①m<0时,∵ 两根异号,∴必有一个负根.
两根异号,∴必有一个负根.
②m>0时,由 时,方程有两正根.综上得
时,方程有两正根.综上得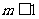 .
.
(2)∵t=-m+2 ,∴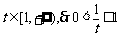 .当t=1时,
.当t=1时,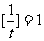 ,当t>1时,
,当t>1时,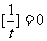 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com