
16.如图: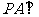 平面
平面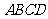 ,四边形
,四边形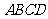 是矩形,
是矩形,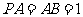 ,点
,点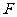 是
是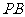 的中点,点
的中点,点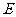 在边
在边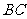 上移动.
上移动.
(1)当点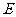 为
为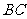 的中点时,试判断
的中点时,试判断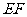 与平面
与平面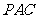 的位置关系,并说明理由;
的位置关系,并说明理由;
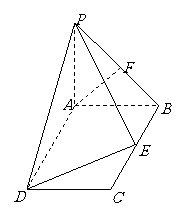 (2)证明:不论点
(2)证明:不论点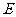 在边
在边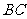 上何处,都有
上何处,都有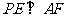 ;
;
15. 设函数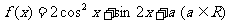 .
.
(Ⅰ)求函数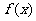 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)当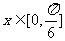 时,f(x)的最大值为2,求a的值,并求出y=f(x)(x∈R)的对称轴方程.
时,f(x)的最大值为2,求a的值,并求出y=f(x)(x∈R)的对称轴方程.
14. 已知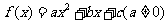 ,且方程
,且方程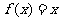 无实数根,下列命题:
无实数根,下列命题:
①方程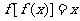 也一定没有实数根;
也一定没有实数根;
②若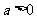 ,则不等式
,则不等式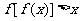 对一切实数
对一切实数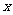 都成立;
都成立;
③若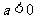 ,则必存在实数
,则必存在实数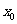 ,使
,使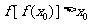
④若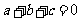 ,则不等式
,则不等式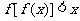 对一切实数
对一切实数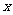 都成立.
都成立.
中,正确命题的序号是 .(把你认为正确的命题的所有序号都填上)
13.过抛物线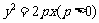 的焦点
的焦点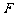 的直线交抛物线于点
的直线交抛物线于点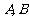 ,交其准线于点
,交其准线于点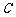 (
(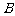 在
在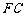 之间),且
之间),且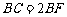 ,
,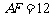 ,则
,则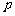 的值为
的值为
12. 随机地向半圆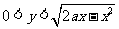 (
(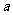 为正常数)内掷一点,点落在圆内任何区域的概率与区域的面积成正比,则原点与该点的连线与
为正常数)内掷一点,点落在圆内任何区域的概率与区域的面积成正比,则原点与该点的连线与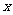 轴的夹角小于
轴的夹角小于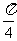 的概率为__________
的概率为__________
11. 设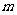 、
、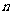 是异面直线,则(1)一定存在平面
是异面直线,则(1)一定存在平面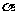 ,使
,使 且
且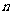 ∥
∥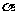 ;(2)一定存在平面
;(2)一定存在平面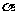 ,使
,使 且
且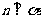 ;(3)一定存在平面
;(3)一定存在平面 ,使
,使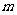 ,
,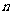 到
到 的距离相等;(4)一定存在无数对平面
的距离相等;(4)一定存在无数对平面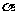 与
与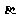 ,使
,使 ,
,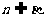 ,且
,且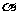 ∥
∥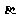 ;上述4个命题中正确命题的序号为 __________
;上述4个命题中正确命题的序号为 __________
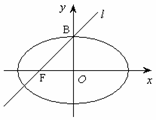
10.设直线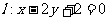 过椭圆的左焦点F和一个顶点B(如图所示),
过椭圆的左焦点F和一个顶点B(如图所示),
则这个椭圆的离心率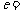 __________.
__________.
9. 已知数列{an}共有m项,记{an}的所有项和为s(1),第二项及以后所有项和为s(2),第三项及以后所有项和为s(3),…,第n项及以后所有项和为s(n),若s(n)是首项为1,公差为2的等差数列的前n项和,则当n<m时,an =
.
已知数列{an}共有m项,记{an}的所有项和为s(1),第二项及以后所有项和为s(2),第三项及以后所有项和为s(3),…,第n项及以后所有项和为s(n),若s(n)是首项为1,公差为2的等差数列的前n项和,则当n<m时,an =
.
8.已知函数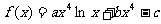 (x>0)在x = 1处取得极值
(x>0)在x = 1处取得极值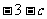 ,其中a,b,c为常数则函数f(x)的单调减区间为__________
,其中a,b,c为常数则函数f(x)的单调减区间为__________
7.设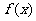 是定义在
是定义在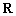 上的奇函数,且当
上的奇函数,且当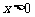 时,
时,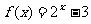 ,则
,则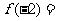
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com