
1.(本题满分12分)
已知函数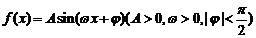 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数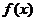 的解析式;
的解析式;
 (Ⅱ)令
(Ⅱ)令 ,判断函数
,判断函数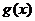 的奇偶性,并说明理由.
的奇偶性,并说明理由.
6.(本小题满分14分)
解:(Ⅰ)∵  ,
, ,
, ,
, ,
,
∴  ;
;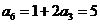 ;
; . ………………3分
. ………………3分
(Ⅱ)由题设,对于任意的正整数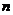 ,都有:
,都有: ,
,
∴ 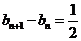 .∴ 数列
.∴ 数列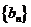 是以
是以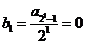 为首项,
为首项,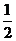 为公差的等差数列.
为公差的等差数列.
∴ 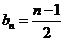 . …………………………………………………………7分
. …………………………………………………………7分
(Ⅲ)对于任意的正整数 ,
,
当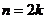 或
或 时,
时, ;
;
当 时,
时, ;
;
当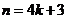 时,
时,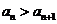 . ……………………………………8分
. ……………………………………8分
证明如下:
首先,由 可知
可知 时,
时, ;
;
其次,对于任意的正整数 ,
,
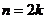 时,
时, ;
;
…………………9分
 时,
时,

所以, . …………………10分
. …………………10分
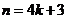 时,
时,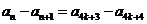
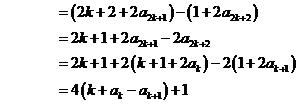
事实上,我们可以证明:对于任意正整数 ,
,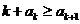 (*)(证明见后),所以,此时,
(*)(证明见后),所以,此时,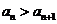 .
.
综上可知:结论得证. …………………12分
对于任意正整数 ,
,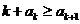 (*)的证明如下:
(*)的证明如下:
1)当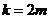 (
( )时,
)时,
 ,
,
满足(*)式。
2)当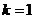 时,
时, ,满足(*)式。
,满足(*)式。
3)当 时,
时,

于是,只须证明 ,如此递推,可归结为1)或2)的情形,于是(*)得证.
,如此递推,可归结为1)或2)的情形,于是(*)得证.
5.(本小题满分13分)
解:(Ⅰ)设椭圆的方程为 ,由题意可得:
,由题意可得:
椭圆C两焦点坐标分别为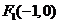 ,
, . .……………1分
. .……………1分
 . .……………3分
. .……………3分
 又
又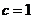
 , ……………4分
, ……………4分
故椭圆的方程为 . .……………5分
. .……………5分
(Ⅱ)当直线
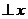 轴,计算得到:
轴,计算得到: ,
,
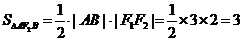 ,不符合题意. .……………6分
,不符合题意. .……………6分
当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为:
的方程为: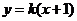 ,
,
由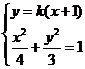 ,消去y得
,消去y得  , .……………7分
, .……………7分
显然 成立,设
成立,设 ,
,
则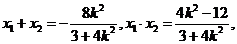 .……………8分
.……………8分
又
即 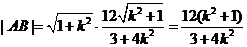 ,
.……………9分
,
.……………9分
又圆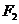 的半径
的半径 .……………10分
.……………10分
所以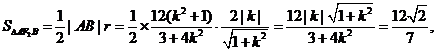
化简,得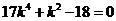 ,
,
即 ,解得
,解得
所以, , .……………12分
, .……………12分
故圆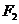 的方程为:
的方程为: . .……………13分
. .……………13分
(Ⅱ)另解:设直线 的方程为
的方程为 
 ,
,
由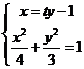 ,消去x得
,消去x得
 ,
, 恒成立,
恒成立,
设 ,则
,则 ……………8分
……………8分
所以 
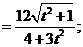
.……………9分
又圆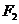 的半径为
的半径为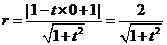 , .……………10分
, .……………10分
所以 ,解得
,解得 ,
,
所以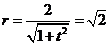 , ……………12分
, ……………12分
故圆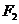 的方程为:
的方程为: . .……………13分
. .……………13分
4.(本小题满分14分)
解:(Ⅰ)当 时,
时,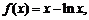
得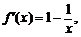 ………………2分
………………2分
令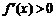 ,即
,即 ,解得
,解得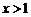 ,所以函数
,所以函数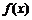 在
在 上为增函数,
上为增函数,
据此,函数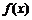 在
在 上为增函数, ………………4分
上为增函数, ………………4分
而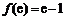 ,
, ,
, 所以函数
所以函数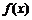 在
在 上的值域为
上的值域为
 ………………6分
………………6分
(Ⅱ)由 令
令 ,得
,得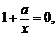 即
即
当 时,
时,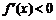 ,函数
,函数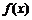 在
在 上单调递减;
上单调递减;
当 时,
时,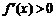 ,函数
,函数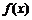 在
在 上单调递增; ……………7分
上单调递增; ……………7分
若 ,即
,即 ,易得函数
,易得函数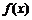 在
在 上为增函数,
上为增函数,
此时, ,要使
,要使 对
对 恒成立,只需
恒成立,只需 即可,
即可,
所以有 ,即
,即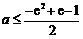
而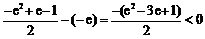 ,即
,即 ,所以此时无解.
,所以此时无解.
………………8分
若 ,即
,即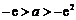 ,易知函数
,易知函数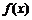 在
在 上为减函数,在
上为减函数,在 上为增函数,
上为增函数,
要使 对
对 恒成立,只需
恒成立,只需 ,即
,即 ,
,
由 和
和
得 . ………………10分
. ………………10分
若 ,即
,即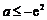 ,易得函数
,易得函数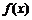 在
在 上为减函数,
上为减函数,
此时, ,要使
,要使 对
对 恒成立,只需
恒成立,只需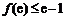 即可,
即可,
所以有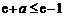 ,即
,即 ,又因为
,又因为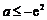 ,所以
,所以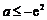 . ……………12分
. ……………12分
综合上述,实数a的取值范围是 . ……………13
. ……………13
3. (本小题满分14分)
解:(Ⅰ)证明:因为 ,且O为AC的中点,
,且O为AC的中点,
所以 . ………………1分
. ………………1分
又由题意可知,平面 平面
平面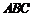 ,交线为
,交线为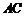 ,且
,且 平面
平面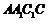 ,
,
所以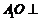 平面
平面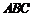 . ………………4分
. ………………4分
(Ⅱ)如图,以O为原点, 所在直线分别
所在直线分别 为x,y,z轴建立空间直角坐标系.
为x,y,z轴建立空间直角坐标系.
由题意可知, 又
又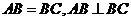

 所以得:
所以得:
则有: ………………6分
………………6分
设平面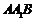 的一个法向量为
的一个法向量为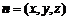 ,则有
,则有
 ,令
,令 ,得
,得
所以 .
………………7分
.
………………7分
 .
………………9分
.
………………9分
因为直线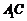 与平面
与平面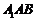 所成角
所成角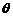 和向量
和向量
 与
与 所成锐角互余,所以
所成锐角互余,所以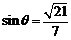 . ………………10分
. ………………10分
(Ⅲ)设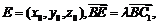 ………………11分
………………11分
即 ,得
,得
所以 得
得 ………………12分
………………12分
令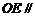 平面
平面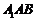 ,得
,得 , ………………13分
, ………………13分
即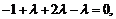 得
得
即存在这样的点E,E为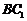 的中点. ………………14分
的中点. ………………14分
2.(本小题满分12分)
解:设指针落在A,B,C区域分别记为事件A,B,C.
则 . ………………3分
. ………………3分
(Ⅰ)若返券金额不低于30元,则指针落在A或B区域.
 ………………6分
………………6分
即消费128元的顾客,返券金额不低于30元的概率是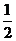 .
.
(Ⅱ)由题意得,该顾客可转动转盘2次.
随机变量 的可能值为0,30,60,90,120. ………………7分
的可能值为0,30,60,90,120. ………………7分

………………10分
所以,随机变量 的分布列为:
的分布列为:
 |
0 |
30 |
60 |
90 |
120 |
 |
 |
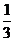 |
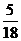 |
 |
 |
………………12分
其数学期望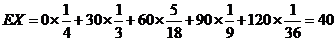 .………13分
.………13分
1.(本小题满分12分)
解:(Ⅰ)由图可知 ,
, , ………………2分
, ………………2分
又由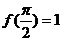 得,
得,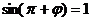 ,又
,又 ,得
,得


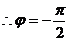 ,
………………4分
,
………………4分
(Ⅱ)由(Ⅰ)知: ………………6分
………………6分
因为
 ………………9分
………………9分
所以,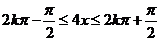 ,即
,即 .……………12分
.……………12分
故函数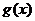 的单调增区间为
的单调增区间为 . ……………13分
. ……………13分
6.(本小题满分14分)
已知数列 满足:
满足: ,
,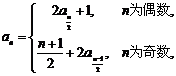 ,
,
(Ⅰ)求 的值;
的值;
(Ⅱ)设 ,试求数列
,试求数列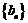 的通项公式;
的通项公式;
(Ⅲ)对于任意的正整数n,试讨论 与
与 的大小关系.
的大小关系.
华侨中学2010届高三解答题限时训练1答案
5.(本小题满分13分)
已知椭圆C的中心在原点,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为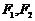 ,且
,且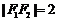 ,点(1,
,点(1,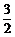 )
)
在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过 的直线
的直线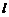 与椭圆
与椭圆 相交于
相交于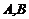 两点,且
两点,且 的面积为
的面积为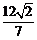 ,求以
,求以 为圆心
为圆心
且与直线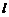 相切的圆的方程.
相切的圆的方程.
4.(本小题满分13分)
已知函数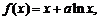 其中a为常数,且
其中a为常数,且 .
.
(Ⅰ)当 时,求
时,求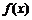 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域;
(Ⅱ)若 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com