
10.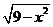 (文科做)已知方程
=x+b有解,则b的取值范围是( )
(文科做)已知方程
=x+b有解,则b的取值范围是( )
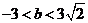
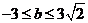 A.|b|<3 B.|b| C.
D.
A.|b|<3 B.|b| C.
D.
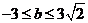
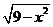 解析:构造函数f(x)= ,
g(x)= x+b,其图像分别为圆的上半部分,及一条动直线,方程有解即为两个函数的图像有公共点,平移直线可知当
时曲线有交点,故选C.
解析:构造函数f(x)= ,
g(x)= x+b,其图像分别为圆的上半部分,及一条动直线,方程有解即为两个函数的图像有公共点,平移直线可知当
时曲线有交点,故选C.
(理科做)集合M={(x,y)|x=3cosθ,y=3sinθ,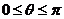 },N={ (x,y)| y= x + b},若M∩N=φ 则b满 足( )
},N={ (x,y)| y= x + b},若M∩N=φ 则b满 足( )
 B
B 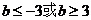
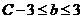
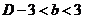
解析:消参数后可得集合M对应的图像同上,故选A.
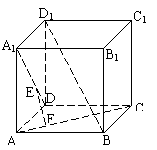
9. 如图,在正方体ABCD-A1B1C1D1中,点E在A1D上且A1E=2ED,点F在AC上且CF=2FA,则EF与BD1的位置关系是( )
A 异面 B 相交 C 垂直 D 平行
解析:过E点作EG平行于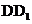 ,交AD于
,交AD于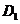 点,连接
点,连接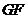 ,由已知可证
,由已知可证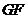 平行于BD,所以可得平面
平行于BD,所以可得平面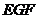 与平面
与平面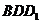 平行,故EF平行于
平行,故EF平行于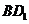 ,选D.
,选D.
8. 设x,y满足约束条件:
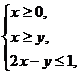 则z=3x+2y的最大值是( )
则z=3x+2y的最大值是( )
A 1 B 2 C 5 D 4
评析:先画出区域,又因为z的几何意义是直线z=3x+2y的纵截距的2倍,平移直线3x+2y=0可得z的最大值为2.
7. 把函数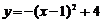 的图象向左平移2个单位,向下平移3个单位,所得的图象所对应的解析式为( )
( )
A.
的图象向左平移2个单位,向下平移3个单位,所得的图象所对应的解析式为( )
( )
A.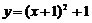 B.
B.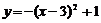 C.
C.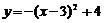 D.
D. 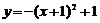
 评析:图像的左右平移及上下平移实质上是改变的x,y,规律是“左加右减”,“上加下减”,故选D。
评析:图像的左右平移及上下平移实质上是改变的x,y,规律是“左加右减”,“上加下减”,故选D。
6. 椭圆上一点A看两焦点的视角为直角,设AF1的延长线交椭圆于B,又|AB|=|AF2|,则椭圆的离心率e为( )
A 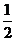 B
B 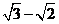 C
C 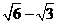 D
D 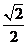 ,
,
解析:设|AB|=|AF2|= x,则由椭圆的定义得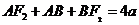 ,即
,即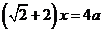 ,
,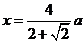
所以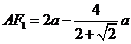 ,结合直角三角形,可得方程
,结合直角三角形,可得方程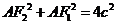 ,解得
,解得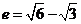 ,选C。
,选C。
5.已知f(x)=(x–a)(x–b)–2(其中a<b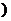 ,且α、β是方程f(x)=0的两根(α<β
,且α、β是方程f(x)=0的两根(α<β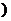 ,则实数a、b、α、β的大小关系为( )
,则实数a、b、α、β的大小关系为( )
A.α<a<b<β B.α<a<β<b C.a<α<b<β D.a<α<β<b
解析:令g(x)= f(x) +2=(x–a)(x–b)(其中a<b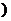 ,可知函数f(x)的图像向上平移2个单位可得函数g(x),而方程g(x)=0的两个跟为a,b,结合图像可知α<a<b<β。
,可知函数f(x)的图像向上平移2个单位可得函数g(x),而方程g(x)=0的两个跟为a,b,结合图像可知α<a<b<β。
4.方程sin(x–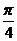 )=
)=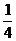 x的实数解的个数是( )
x的实数解的个数是( )
A.2 B.3 C.4 D.以上均不对
解析:由函数与方程思想知:方程的根转化为对应函数图像的交点的横坐标,分别作出函数y=sin(x–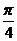 )和函数y=
)和函数y=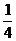 x的图像,由图像知交点个数为3个,故方程的根有3个。
x的图像,由图像知交点个数为3个,故方程的根有3个。
3.设关于x的方程sinx+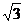 cosx+a=0在(0,π)内有相异解α、β.则a的取值范围是( );
cosx+a=0在(0,π)内有相异解α、β.则a的取值范围是( );
A (–2,–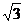 )∪(–
)∪(–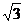 ,2) B (–2,–
,2) B (–2,–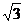 ) C (–
) C (–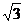 ,2) D 不确定
,2) D 不确定
解析:作出y=sin(x+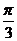 )(x∈(0,π))及y=–
)(x∈(0,π))及y=–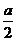 的图象,知当|–
的图象,知当|–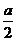 |<1且–
|<1且–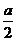 ≠
≠
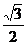 时,曲线与直线有两个交点,故a∈(–2,–
时,曲线与直线有两个交点,故a∈(–2,–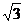 )∪(–
)∪(–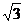 ,2).故选A。
,2).故选A。
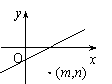
2.如图,直线Ax+By+C=0(AB≠0)的右下方有一点(m,n),则Am+Bn+C的值( )
 A与A同号,与B同号
A与A同号,与B同号
B与A同号,与B异号
C与A异号,与B同号
D与A异号,与B异号
解析:一元二次不等式的几何意义是:表示平面上的区域,由图知AB异号,所以排除选项A,D,不妨设
A>0, 则B<0,C<0,因为点(m,n)在直线的下方,所以Am+Bn+C>0,故选B.
1.设全集U=R,集合A=(1,+∞),集合B=(-∞,2)。则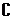 U(A∩B)=( )
U(A∩B)=( )
A.(-∞,1)∪(2,+∞) B.(-∞,1)∪[2,+∞)
C.(-∞,1]∪[2,+∞) D.(-∞,1]∪(2,+∞)
解析:涉及数集的运算,画出数轴可求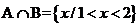 ,进而得
,进而得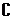 U(A∩B)=(-∞,1]∪[2,+∞);
U(A∩B)=(-∞,1]∪[2,+∞);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com