
2.已知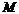 是
是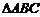 的
的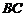 边上的一个三等分点,且
边上的一个三等分点,且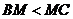 ,若
,若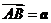 ,
,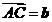 ,则
,则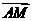 等
等 于。
于。
A.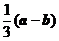 B.
B.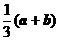 C.
C.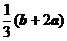 D.
D.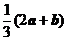
1.化简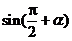 等于.
等于.
A.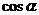
 B.
B.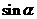 C.
C.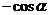 D.
D.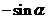
16.(11分)将金属块m用压缩的轻质弹簧卡在一个矩形的箱中,如图13所示,在箱的上顶板和下底板装有压力传感器,箱可以沿竖直轨道运动.当箱以a=2.0 m/s2的加速度竖直向上做匀减速运动时,上顶板的传感器显示的压力为6.0 N,下底板的传感器显示的压力为10.0 N.(取g=10 m/s2)
(1)若上顶板传感器的示数是下底板传感器示数的一半,试判断箱的运动情况.
(2)使上顶板传感器的示数为零,箱沿竖直方向运动的情况可能是怎样的?
解析:上顶板传感器显示的示数为上顶板对金属块的弹力,设为F上,下底板传感器显示的示数为弹簧的弹力,设为F下.
当箱竖直向上做匀减速运动时,则有
F上-F下+mg=ma
即m==0.5 kg.
(1)当上顶板传感器的示数为下底板传感器示数的一半时箱的加速度为a1,因为弹簧长度不变,所以F下不变,则有a1==0
因此,箱处于静止状态或匀速直线运动状态.
(2)当上顶板传感器的示数为零时,设此时箱的加速度为a2,并取竖直向下为正方向,则有
a2==-10.0 m/s2
因此,此时箱的加速度竖直向上,由此得,箱可能向上做匀加速运动,也可能向下做匀减速运动.
答案:(1)箱处于静止状态或匀速直线运动状态
(2)箱可能向上做匀加速运动,也可能向下做匀减速运动
15.(10分)杂技演员在进行“顶竿”表演时,用的是一根质量可忽略不计的长竹竿.质量为m=30 kg的演员自竹竿顶部由静止开始下滑,滑到竹竿底端时速度恰好为零.为了研究下滑演员沿竿的下滑情况,在顶竿演员与竹竿底部之间安装一个传感器.由于竹竿处于静止状态,传感器显示的就是下滑演员所受摩擦力的情况,如图12所示,g取10 m/s2.求:
(1)下滑演员下滑过程中的最大速度;
(2)竹竿的长度.
解析:(1)由图象可知,下滑演员在t1=1 s内匀加速下滑,设下滑的加速度为a,则根据牛顿第二定律,有mg-F=ma
a== m/s2=4 m/s2
1 s末下滑演员的速度达最大
vm=at1=4 m/s.
(2)由图象可知,1 s末-3 s末下滑演员做匀减速运动,末速度为零,则杆长为L=vm(t1+t2)=×4×(1+2) m=6 m或a′== m/s2=2 m/s2
L=at+(vmt2-a′t)=6 m.
答案:(1)4 m/s (2)6 m

图13
14.(10分)如图11所示,固定在水平面上的斜面倾角θ=37°,长方体木块A的MN面上钉着一颗小钉子,质量m=1.5 kg的小球B通过一细线与小钉子相连接,细线与斜面垂直,木块与斜面间的动摩擦因数μ=0.50.现将木块由静止释放,木块将沿斜面下滑.求在木块下滑的过程中小球对木块MN面的压力.(取g=10 m/s2,sin37°=0.6,cos37°=0.8)
解析:由于木块与斜面间有摩擦力的作用,所以小球B与木块间有压力的作用,并且它们以共同的加速度a沿斜面向下运动.将小球和木块看做一个整体,设木块的质量为M,根据牛顿第二定律可得(M+m)gsinθ-μ(M+m)gcosθ=(M+m)a
代入数据得a=2.0 m/s2
选小球为研究对象,设MN面对小球的作用力为FN,
根据牛顿第二定律有mgsinθ-FN=ma
代入数据得FN=6.0 N
根据牛顿第三定律,小球对MN面的压力大小为6.0 N,方向沿斜面向下.
答案:6.0 N,方向沿斜面向下
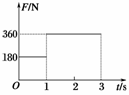
图12
13.(9分)近日教育部出台了一系列加强中学生体育锻炼的措施,其中跳起摸高是中学生进行的一项体育活动.某同学身高1.80 m,质量65 kg,站立举臂手指摸到的高度是2.25 m,此同学用力蹬地竖直跳离地面历经0.3 s,设他蹬地时的力大小恒定为1300 N,求该同学(g取10 m/s2):
(1)刚跳离地面时的速度;
(2)跳起可摸到的高度.
解析:设该同学刚跳离地面时的速度为v,跳离地面后,上升的最大高度为h,则
(1)由题意可知该同学在跳离地面的过程中,做的是匀加速直线运动,由牛顿第二定律可得:
FN-mg=ma
由运动学公式,可得v=at
代入数据解得v=3 m/s.
(2)该同学自跳离地面到上升至最高点,做竖直上抛运动:h== m=0.45 m
该同学跳起可摸到的高度
H=L+h=2.25 m+0.45 m=2.70 m.
答案:(1)3 m/s (2)2.70 m
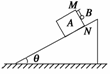
图11
12.(10分)某探究性学习小组欲探究光滑斜面上物体下滑的加速度与物体质量及斜面倾角是否有关.实验室提供如下器材:
A.表面光滑的长木板(长度为L);
B.小车;
C.质量为m的钩码若干个;
D.方木块(备用于垫木板);
E.米尺;F.秒表.
实验过程:
第一步,在保持斜面倾角不变时,探究加速度与质量的关系.实验中,通过向小车放入钩码来改变物体质量,只要测出小车由斜面顶端滑至底端所用时间t,就可以由公式a=________求出a.
某同学记录的数据如下表所示:
 |
M |
M+m |
M+2m |
|
1 |
1.42 |
1.41 |
1.42 |
|
2 |
1.40 |
1.42 |
1.39 |
|
3 |
1.41 |
1.38 |
1.42 |
根据以上信息,我们发现,在实验误差范围内质量改变之后平均下滑时间________(填“改变”或“不改变”),经过分析得出加速度与质量的关系为________.第二步,在物体质量不变时,探究加速度与倾角的关系.实验中通过改变方木块垫放位置来调整长木板的倾角,由于没有量角器,因此通过测量出木板顶端到水平面高度h,求出倾角α的正弦值sinα=h/L.
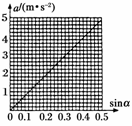
图9
某同学记录了高度和加速度的对应值,并在坐标纸上建立适当的坐标轴后描点作图如图9,请根据他所作的图线求出当地的重力加速度g=________m/s2.进一步分析可知,光滑斜面上物体下滑的加速度与倾角的关系为________.
解析:斜面长度L已知,测出小车由斜面顶端运动到斜面底端的时间t,由L=at2得a=
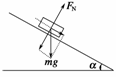
图10
分析表中数据,发现小车质量改变时,下滑时间不变(略有不同是因为实验中存在误差).因此加速度与质量无关.
小车沿光滑斜面下滑时,受力如图10.
则ma=mgsinα
所以a=gsinα(可见与质量无关)
则a-sinα图象中图线的斜率表示g的大小.由图象中取两点,读出其横、纵坐标(sinα1,α1)、(sinα2,α2),那么g=
例如g= m/s2=9.80 m/s2.
答案: 不改变 无关 9.80 a=gsinα
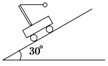
图7
11.(10分)如图7所示,在倾角为30°的斜面上,一辆动力小车沿斜面下滑,在小车下滑的过程中,小车支架上连接着小球的轻绳恰好水平.已知小球的质量为m,则小车运动的加速度大小为________,绳对小球的拉力大小为________.
解析:
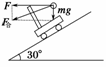
图8
对小球受力分析如图8,小球的加速度沿斜面向下,由牛顿第二定律得a===2g
由图可得:
F=mg·cot30°=mg.
答案:2g mg
10.(2009年福建福州质检)商场搬运工要把一箱苹果沿倾角为θ的光滑斜面推上水平台,如图6所示.他由斜面底端以初速度v0开始将箱推出(箱与手分离),这箱苹果刚好能滑上平台.箱子的正中间是一个质量为m的苹果,在上滑过程中其他苹果对它的作用力大小是( )
A.mg B.mgsinθ
C.mgcosθ D.0
解析:以箱子和里面所有苹果作为整体为研究,受力分析得,Mgsinθ=Ma,则a=gsinθ,方向沿斜面向下;再以苹果为研究对象,受力分析得,合外力F=ma=mgsinθ,与苹果重力沿斜面的分力相同,由此可知,其他苹果给它的力应与重力垂直于斜面的分力相等,即mgcosθ,故C正确.
答案:C
第Ⅱ卷 非选择题
9.如图5所示,完全相同的容器E、F、G,小孔a与大气相通,容器口封闭,T为阀门,水面的高度相同.在E静止、F、G同时竖直向上和向下以加速度a运动的同时打开三个容器的阀门,则以上说法中正确的是( )
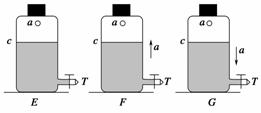
图5
A.从三个容器阀门流出的水速大小关系是vE<vF<vG
B.从三个容器阀门流出的水速大小关系是vE>vF>vG
C.水有可能不从G容器的T阀门中流出
D.从三个容器阀门流出的水速大小关系可能是vF>vG>vE
解析:F容器处于超重状态;G容器处于失重状态,所以vF>vE>vG,当a=g处于完全失重状态时水就不会从孔流出.
答案:C
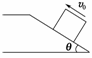
图6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com