
1.p:a2>b2 q:a>b 则p是q的 既不充分也不必要条件 。
2.在同一平面内一直线的垂线与斜线一定相交。
|
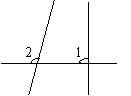 如图,设l1与l2相交所得的一对同位角为Ð1和Ð2
如图,设l1与l2相交所得的一对同位角为Ð1和Ð2
则Ð1=Ð2 ∵l2是l的斜线 ∴Ð2¹90°
|
说明l1与l的交角不是直角,这与l1^l矛盾
∴l1和l2一定相交。
1.已知a与b均为有理数,且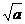 和
和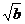 都是无理数,证明
都是无理数,证明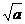 +
+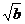 也是无理数。
也是无理数。
证明:假设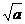 +
+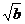 是有理数,则(
是有理数,则(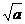 +
+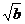 )(
)(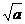 -
-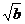 )=a-b
)=a-b
由a>0, b>0 则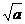 +
+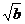 >0 即
>0 即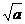 +
+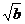 ¹0
¹0
∴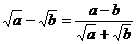 ∵a,bÎQ 且
∵a,bÎQ 且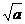 +
+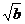 ÎQ
ÎQ
∴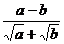 ÎQ 即(
ÎQ 即(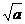 -
-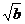 )ÎQ
)ÎQ
这样(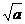 +
+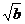 )+(
)+(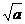 -
-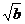 )=2
)=2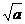 ÎQ
ÎQ
从而 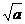 ÎQ (矛盾) ∴
ÎQ (矛盾) ∴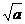 +
+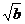 是无理数。
是无理数。
2.若xy=0则x=0或y=0
解:命题的否定:xy=0且x¹0又y¹0。(假命题)
否命题:若xy¹0则x¹0且y¹0。(真命题)
1.若x,y都是奇数,则x+y是偶数。
解:命题的否定:x,y都是奇数且x+y不是偶数。(假命题)
否命题:若x,y不都是奇数,则x+y不是偶数。(假命题)
4.若mn<0,则方程mx2-x+n=0有两个不相等的实数根。
解:逆命题:若方程mx2-x+n=0有两个不等实数根,则mn<0。(假命题)
否命题:若mn≥0,则方程mx2-x+n=0没有两个不等实数根。(假命题)
逆否命题:若方程mx2-x+n=0没有两个不等实数根,则mn≥0。(真命题)
3.当c<0时,若ac>bc则a<b。
解:逆命题:当c<0时,若a<b则ac>bc。(真命题)
否命题:当c<0时,若ac≤bc则a≥b。(真命题)
逆否命题:当c<0时,若a≥b则ac≤bc。(真命题)
2.若x=0则xy=0。
解:逆命题:若xy=0则x=0。(假命题)
否命题:若x¹0则xy¹0。(假命题)
逆否命题:若xy¹0则x¹0。(真命题)
1.面积相等的两个三角形是全等三角形。
解:逆命题:两个全等三角形面积相等。(真命题)
否命题:面积不等的两个三角形不是全等三角形。(真命题)
逆否命题:不全等的两个三角形面积不相等。(假命题)
4.弦的垂直平分线经过圆心,并平分弦所对的弧。
解:若一条直线是弦的垂直平分线,则这条直线经过圆心且平分弦所对的弧。 (真命题)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com