2．(2010 江苏镇江)计算：-3+2=　　　 ；　　　　　　　　　　　　　　　 (-3)×2=　　　　 .

[答案]-1，-6

1．(2010江苏镇江)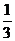的倒数是　　　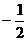　 ；　　　　　　　　　　　　　　　 的相反数是　　　　 .

[答案]3，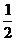

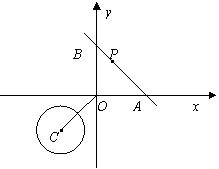
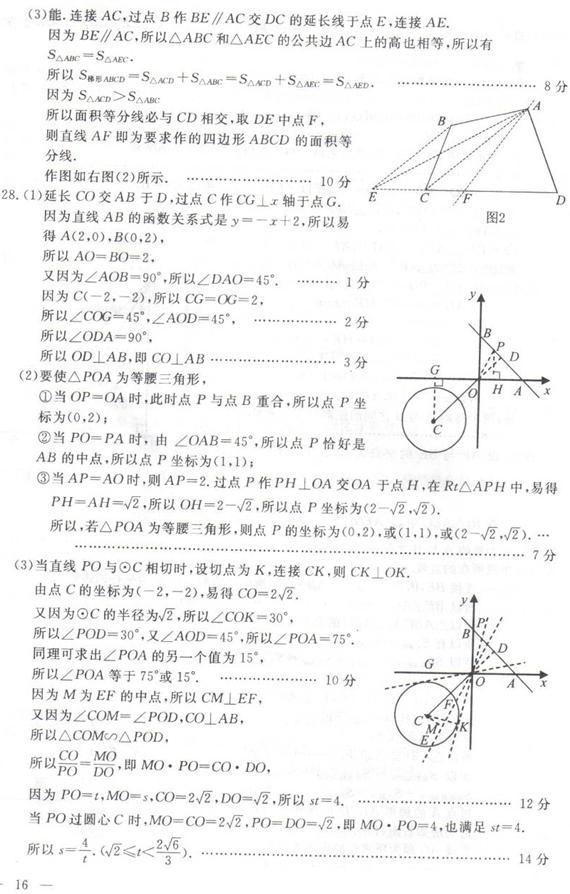
28．(本题满分14分)如图，在平面直角坐标系中，O为坐标原点，⊙C的圆心坐标为(－2，－2)，半径为．函数y＝－x+2的图象与x轴交于点A，与y轴交于点B，点P为AB上一动点

(1)连接CO，求证：CO⊥AB；

(2)若△POA是等腰三角形，求点P的坐标；

(3)当直线PO与⊙C相切时，求∠POA的度数；当直线PO与⊙C相交时，设交点为E、F，点M为线段EF的中点，令PO＝t，MO＝s，求s与t之间的函数关系，并写出t的取值范围．

27．(本题满分10分)如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的一条面积等分线．如，平行四边形的一条对角线所在的直线就是平行四边形的一条面积等分线．

(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________；

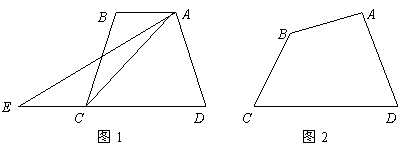
(2)如图1，梯形ABCD中，AB∥DC，如果延长DC到E，使CE＝AB，连接AE，那么有S_梯形ABCD＝S_△ADE．请你给出这个结论成立的理由，并过点A作出梯形ABCD的面积等分线(不写作法，保留作图痕迹)；

(3)如图，四边形ABCD中，AB与CD不平行，S_△ADC＞S_△ABC，过点A能否作出四边形ABCD的面积等分线？若能，请画出面积等分线，并给出证明；若不能，说明理由．

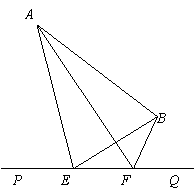
26．(本题满分10分)如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，∠BFQ＝60°，EF＝1km．

(1)判断AB与AE的数量关系，并说明理由；

(2)求两个岛屿A和B之间的距离(结果精确到0.1km)．(参考数据：≈1.73，sin74°≈0.96，

cos74°≈0.28，tan74°≈3.49，sin76°≈0.97，cos76°≈0.24)

25．(本题满分10分)我市某工艺品厂生产一款工艺品．已知这款工艺品的生产成本为每件60元．经市场调研发现：该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系．

(利润＝(售价－成本价)×销售量)

(1)求销售量y(件)与售价x(元)之间的函数关系式；

(2)你认为如何定价才能使工艺品厂每天获得的利润为40 000 元？

24．(本题满分10分)如图，正方形网格中的每一个小正方形的边长都是1，四边形ABCD的四个顶点都在格点上，O为AD边的中点，若把四边形ABCD绕着点O顺时针旋转180°．试解决下列问题：

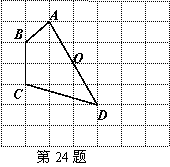　(1)画出四边形ABCD旋转后的图形；

(2)求点C旋转过程中所经过的路径长；

(3)设点B旋转后的对应点为B’，求tan∠DAB’的值．

23．(本题满分10分)在一次数学测验中，甲、乙两校各有100名同学参加测试．测试结果显示，甲校男生的优分率为60%，女生的优分率为40%，全校的优分率为49.6%；乙校男生的优分率为57%，女生的优分率为37%．

(男(女)生优分率＝×100%，全校优分率＝×100%)

(1)求甲校参加测试的男、女生人数各是多少？

(2)从已知数据中不难发现甲校男、女生的优分率都相应高于乙校男、女生的优分率，但最终的统计结果却显示甲校的全校优分率比乙校的全校的优分率低，请举例说明原因．

22．(本题满分8分)已知反比例函数y＝的图象与二次函数y＝ax²+x－1的图象相交于点(2，2)

(1)求a和k的值；

(2)反比例函数的图象是否经过二次函数图象的顶点，为什么？

21．(本题满分8分)从甲地到乙地有A₁、A₂两条路线，从乙地到丙地有B₁、B₂、B₃三条路线，从丙地到丁地有C₁、C₂两条路线．一个人任意先了一条从甲地到丁地的路线．求他恰好选到B₂路线的概率是多少？