
5.(2009重庆卷)在下面横线处各补上一句话。要求:语意连贯,句式一致,形成完整的排比句。
人要懂得尊重自己,尊重自己所以不苟且,不苟且所以有品位;人要懂得尊重别人, ,
;人要懂得尊重自然, , 。
[答案]尊重别人所以不傲慢,不傲慢所以有品位。尊重自然所以不自大,不自大所以有自知。
[解析]题目明确要求将补写的句子写成排比句,但考生不要只看到这一点,细看给出的句子,还有顶针的特点,即前一句话的最后一个短语必须位于后一句话的最前面,因此,仿写时,除了看题目要求外,还要看被仿写的句子的结构特点。
[考点定位]此题考查考生仿写句子的能力,能力层级为D。
4.(2009四川卷)仿照下面这句话,另选一种景物进行描写。要求句式基本一致,并运用比拟、比喻和排比的修辞手法。
层层的叶子中间,零星地点缀着些白花,有袅娜地开着的,有羞涩地打着朵儿的;正如一粒粒的明珠,又如碧天里的星星,又如刚出浴的美人。
答:
。
[答案]示例:悠悠白云中,隐约地横亘着一座座青山;有腼腆地躲进雾霭的,有大方地露出真容的;正如一把把直刺苍穹的利剑,又如碧空中飞腾的巨龙,又如绵延不断的绿色屏障。
[解析]该题主要考查学生熟练运用比拟比喻和排比的修辞。此外还要注意句式的一致性,讲求一点文采。
[考点定位]本题主要考察学生的仿写能力以及一定的语言文采。
3.(2009湖北卷)为庆祝新中国成立60周年,学校拟编辑出版诗歌征文集。现有两个备选书名《献给母亲的歌》和《山河岁月欢乐颂》,你喜欢哪一个?请写下你喜欢的书名并说明理由。
我喜欢的书名:《 》
理由:
。
[答案]示例:①我喜欢的书名:《献给母亲的歌》。理由:把祖国比喻为母亲,给母亲献歌,表达了对祖国母亲的深爱,直抒胸臆,情真意切。②我喜欢的书名:《山河岁月欢乐颂》。理由:山河是祖国的代表,岁月是祖国的历程,欢乐颂是我们赞美祖国的共同心声。
[解析]诗歌集的主题思想史“为庆祝新中国成立60周年”,所以①两个标题中都使用了修辞手法,前者是比喻,后者是借代;②这种含蓄的表达风格,前者更强烈直接地抒发了对祖国母亲的深爱,后者委婉深沉地抒发我们赞美祖国的共同心声。
[考点定位]本体考查正确运用常见修辞方法的能力,能力层级为D。做这种题,一要掌握常见的修辞方法(比喻、比拟、借代、夸张、对偶、排比、反复、反问、设问等)的一般作用和效果;二药理解具体语境中运用修辞方法的语句的含意。
2.(2009全国卷II)仿照下面的事例,自选话题,写出三个句子,要求所写句子形成排比,句式与示例相同。
金钱不必车载斗量,够用就好;友谊不必甜言蜜语,真诚就好;人生不必惊天动地,踏实就好。
答:
。
[答案]房屋不必豪宅别墅,舒适即可;朋友不必前呼后拥,知心即可;生活不必波澜起伏,平淡即可。
[定位]本题重点考查考生仿用句式的能力,要特别注意暗示信息的处理,一是内容上,不“破”不“立”,“破”“立”结合,先否定后肯定;二是感情基调上一定要切合要求,昂扬向上,健康主流。
[解析]注意例句形式“……不必……,……就好”,要形成排比;内容上注意相关性。
1.(2009全国卷I)仿照下面的示例,自选话题,另写三个句子,要求所写句子形成排比,句式与例相同。
工作是等不来的,有无机会,看你怎么争取;业绩是要不来的,有无成效,看你怎么努力;前途是盼不来的,有无出路,看你怎么奋斗。
答:
。
[答案]机会是盼不来的,有无运气,看你如何行动;机遇是碰不到的,有无可能,看你怎样追求;成功是等不来的,能否实现,看你如何突破。
[定位]本题重点考查考生仿用句式的能力,能力层级为D。
[解析]要特别注意示例句形式,同时也要注意语段在内容上应相成递减或递增的排比关系,整个情感基调为赞扬或表彰的。“工作”“业绩”“前途”有递进关系。
17.(2010湖南文数) (本小题满分12分)
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
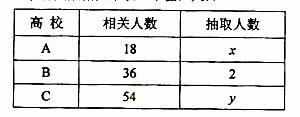
(I) 求x,y ;
(II) 若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率。


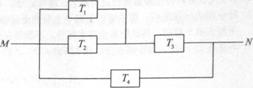
(2010全国卷2理数)(20)(本小题满分12分)
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
(Ⅰ)求p;
(Ⅱ )求电流能在M与N之间通过的概率;
)求电流能在M与N之间通过的概率;
(Ⅲ)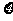 表示T1,T2,T3,T4中能通过电流的元件个数,求
表示T1,T2,T3,T4中能通过电流的元件个数,求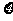 的期望.
的期望.
[命题意图]本试题主要考查独立事件的概率、对立事件的概率、互斥事件的概率及数学期望,考查分类讨论的思想方法及考生分析问题、解决问题的能力.
19.(2010湖南文数)(本小题满分13分)
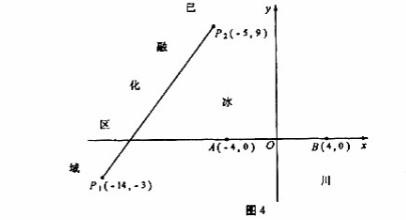
为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(图4)。考察范围到A、B两点的距离之和不超过10Km的区域。
(I) 求考察区域边界曲线的方程:
(II)
如图4所示,设线段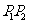 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?
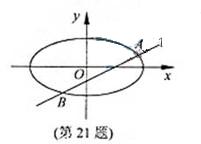
 (2010浙江理数)(21) (本题满分15分)已知m>1,直线
(2010浙江理数)(21) (本题满分15分)已知m>1,直线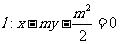 ,椭圆
,椭圆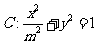 ,
, 分别为椭圆
分别为椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线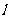 过右焦点
过右焦点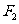 时,求直线
时,求直线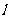 的方程;
的方程;
(Ⅱ)设直线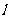 与椭圆
与椭圆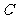 交于
交于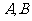 两点,
两点,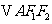 ,
,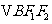 的重心分别为
的重心分别为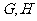 .若原点
.若原点 在以线段
在以线段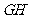 为直径的圆内,求实数
为直径的圆内,求实数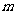 的取值范围.
的取值范围.
解析:本题主要考察椭圆的几何性质,直线与椭圆,点与圆的位置关系等基础知识,同时考察解析几何的基本思想方法和综合解题能力。
(Ⅰ)解:因为直线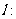
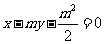 经过
经过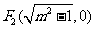 ,所以
,所以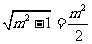 ,得
,得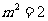 ,
,
又因为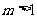 ,所以
,所以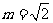 ,
,
故直线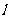 的方程为
的方程为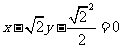 。
。
 (Ⅱ)解:设
(Ⅱ)解:设 。
。
由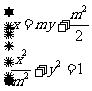 ,消去
,消去 得
得
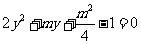
则由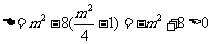 ,知
,知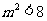 ,
,
且有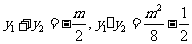 。
。
由于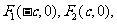 ,
,
故 为
为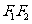 的中点,
的中点,
由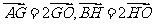 ,
,
可知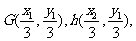
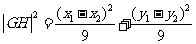
设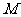 是
是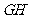 的中点,则
的中点,则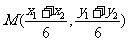 ,
,
由题意可知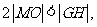
即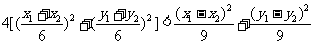
即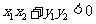
而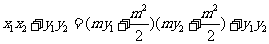
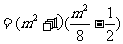
所以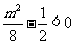
即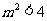
又因为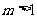 且
且
所以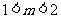 。
。
所以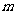 的取值范围是
的取值范围是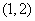 。
。
(2010全国卷2理数)(21)(本小题满分12分)
己知斜率为1的直线l与双曲线C: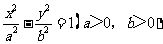 相交于B、D两点,且BD的中点为
相交于B、D两点,且BD的中点为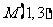 .
.
(Ⅰ)求C的离心率;
(Ⅱ)设C的右顶点为A,右焦点为F,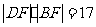 ,证明:过A、B、D三点的圆与x轴相切.
,证明:过A、B、D三点的圆与x轴相切.
[命题意图]本题主要考查双曲线的方程及性质,考查直线与圆的关系,既考查考生的基础知识掌握情况,又可以考查综合推理的能力.
15、(2010江苏卷)(本小题满分14分)
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C( -2
-2
 ,-1)。
,-1)。
(3)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(4)设实数t满足(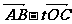 )·
)·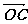 =0,求t的值。
=0,求t的值。
[解析]本小题考查平面向量的几何意义、线性运算、数量积,考查运算求解能力。满分14分。
(1)(方法一)由题设知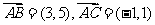 ,则
,则
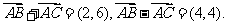
所以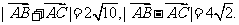
故所求的两条对角线的长分别为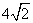 、
、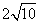 。
。
(方法二)设该平行四边形的第四个顶点为D,两条对角线的交 点为
点为 E,则:
E,则:
E为B、C的中点,E(0,1)
又E(0,1)为A、D的中点,所以D(1,4)
故所求的 两条对角线的长分别为B
两条对角线的长分别为B C=
C=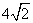 、AD=
、AD=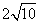 ;
;
(2)由题设知: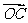 =(-2,-1),
=(-2,-1),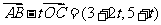 。
。
由(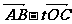 )·
)·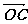 =0,得:
=0,得: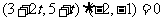 ,
,
从而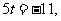 所以
所以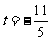 。
。
或者: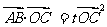 ,
,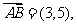
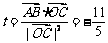
15、(2010江苏卷)(本小题满 分14分)
分14分)
在 平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(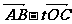 )·
)·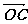 =0,求t的值。
=0,求t的值。
[解析]本小题考查平面向量的几何意义 、线性运算、数量积,考查运算求解能力。满分14分。
、线性运算、数量积,考查运算求解能力。满分14分。
(1)(方法一 )由题设知
)由题设知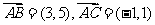 ,则
,则
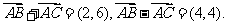
所以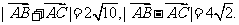
故所求的两条对角线的长分别为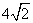 、
、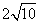 。
。
(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:
 E为B、C的中点,E(0,1)
E为B、C的中点,E(0,1)
又E(0,1)为A、D的中点,所以D(1,4)
故所求的两条对角线的长分别为BC=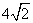 、AD=
、AD=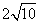 ;
;
(2)由题设知: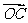 =(-2
=(-2 ,-1),
,-1),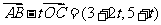 。
。
由(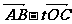 )·
)·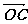 =0,得:
=0,得: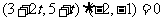 ,
,
从而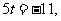 所以
所以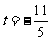 。
。
或 者:
者: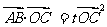 ,
,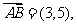
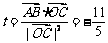
21.(2010湖南文数)(本小题满分13分)
已知函数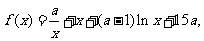 其中a<0,且a≠-1.
其中a<0,且a≠-1.
(Ⅰ)讨论函数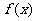 的单调性;
的单调性;
(Ⅱ)设函数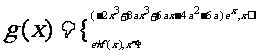 (e是自然数的底数)。是否存在a,使
(e是自然数的底数)。是否存在a,使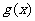 在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。



(2010浙江理数) (22)(本题满分14分)已知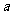 是给定的实常数,设函数
是给定的实常数,设函数 ,
,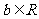 ,
,
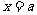 是
是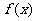 的一个极大值点.
的一个极大值点.
(Ⅰ)求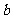 的取值范围;
的取值范围;
(Ⅱ)设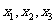 是
是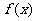 的3个极值点,问是否存在实数
的3个极值点,问是否存在实数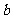 ,可找到
,可找到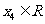 ,使得
,使得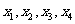 的某种排列
的某种排列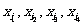 (其中
(其中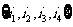 =
=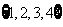 )依次成等差数列?若存在,求所有的
)依次成等差数列?若存在,求所有的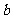 及相应的
及相应的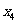 ;若不存在,说明理由.
;若不存在,说明理由.
解析:本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论证能力、分类讨论等综合解题能力和创新意识。
(Ⅰ)解:f’(x)=ex(x-a)
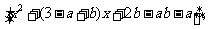
令
于是,假设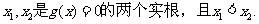
(1) 当x1=a 或x2=a时,则x=a不是f(x)的极值点,此时不合题意。
(2) 当x1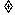 a且x2
a且x2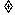 a时,由于x=a是f(x)的极大值点,故x1<a<x2.
a时,由于x=a是f(x)的极大值点,故x1<a<x2.
即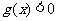
即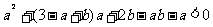
所以b<-a
所以b的取值范围是(-∞,-a)
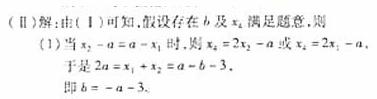
此时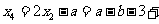

或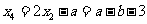

(2)当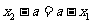 时,则
时,则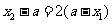 或
或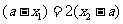
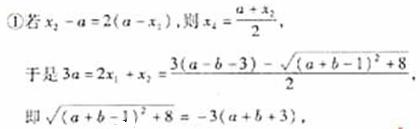
于是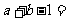
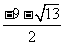
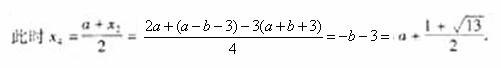
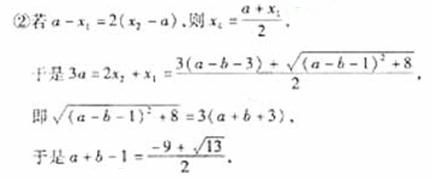
此时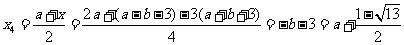
综上所述,存在b满足题意,
当b=-a-3时,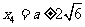
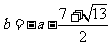 时,
时,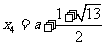
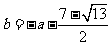 时,
时,
(2010全国卷2理数)(22)(本小题满分12分)
设函数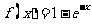 .
.
(Ⅰ)证明:当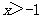 时,
时,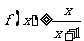 ;
;
(Ⅱ)设当 时,
时,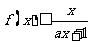 ,求a的取值范围.
,求a的取值范围.
[命题意图]本题主要考查导数的应用和利用导数证明不等式,考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com