
22.(2010上海文数)(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分。
若实数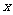 、
、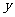 、
、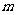 满足
满足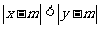 ,则称
,则称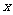 比
比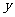 接近
接近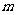 .
.
(1)若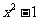 比3接近0,求
比3接近0,求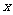 的取值范围;
的取值范围;
(2)对任意两个不相等的正数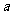 、
、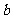 ,证明:
,证明: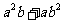 比
比 接近
接近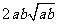 ;
;
(3)已知函数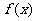 的定义域
的定义域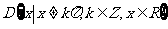 .任取
.任取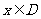 ,
,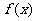 等于
等于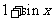 和
和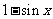 中接近0的那个值.写出函数
中接近0的那个值.写出函数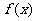 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
解析:(1) xÎ(-2,2);
(2) 对任意两个不相等的正数a、b,有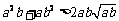 ,
,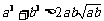 ,
因为
,
因为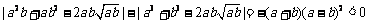 ,
所以
,
所以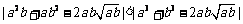 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近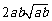 ;
(3)
;
(3) 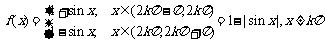 ,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间
,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间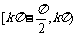 单调递增,在区间
单调递增,在区间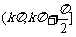 单调递减,kÎZ.
单调递减,kÎZ.
16.(2010湖南文数) (本小题满分12分)
 已知函数
已知函数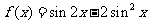
(I)求函数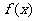 的最小正周期。
的最小正周期。
(II) 求函数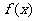 的最大值及
的最大值及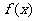 取最大值时x的集合。
取最大值时x的集合。

(2010浙江理数)(18)(本题满分l4分)在△ABC中,角A、B、C所对的边分别为a,b,c,已知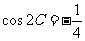
(I)求sinC的值;
(Ⅱ)当a=2, 2sinA=sinC时,求b及c的长.
2sinA=sinC时,求b及c的长.
解析:本题主要考察三角变换、正弦定理、余弦定理等基础知识,同事考查运算求解能力。
(Ⅰ)解:因为cos2C=1-2sin2C=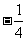 ,及0<C<π
,及0<C<π
所以sinC=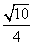 .
.
(Ⅱ)解:当a=2,2sinA=sinC时,由正弦定理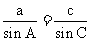 ,得
,得
c=4
由cos2C=2cos2C-1= ,J及0<C<π得
,J及0<C<π得
cosC=±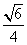
由余弦定理c2=a2+b2-2abcosC,得
b2±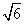 b-12=0
b-12=0
解得
b=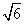 或2
或2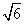
 所以 b=
所以 b=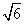 b=
b=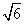
c=4 或 c=4
(2010全国卷2理数)(17)(本小题满分10分)
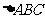 中,
中,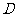 为边
为边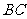 上的一点,
上的一点,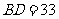 ,
,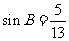 ,
,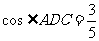 ,求
,求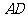 .
.
[命题意图]本试题主要考查同角三角函数关系、两角和差公式和正弦定理在解三角形中的应用,考查考生对基础知识、基本技能的掌握情况.
19.(2010上海文数)(本题满分12分)
已知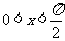 ,化简:
,化简:
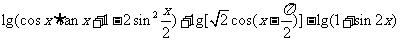 .
.
解析:原式=lg(sinx+cosx)+lg(cosx+sinx)-lg(sinx+cosx)2=0.
2009年8月17日 在德国柏林举行的世锦赛上,牙买加选手博尔特再次打破百米世界记录,再创佳绩。请根据以下要点向21st Century报刊投寄一篇介绍当今百米飞人博尔特的文章:
姓名:尤塞恩-博尔特(Usain Bolt);绰号闪电(Lightning Bolt)
生日:1986年8月21日
国籍:牙买加(Jamaica)
身高:1.96米
职业:田径运动员
性格特征:有天赋,勤奋,有爱心,有毅力;
梦想:再次打破世界记录。
成绩:
2009年8月17日,德国柏林世锦赛,第二次打破100米、200米世界记录;共获3金
2008年8月16日,北京奥运动会,第一次打破100米、200米世界记录;共获3金
写作要求:1.使用必要连接词以使行文连贯;
2.字数为100-120字。
参考词汇:田径 track and field
柏林世锦赛 World Championship in Berlin
Usain Bolt
__________________________________________________________________________________________________________________________________
10. The soldiers __________ the bridge in order to cut off the enemy’s escape into the mountains.
4. Generally speaking, boys ___________ sports, because they love to go out and run.
3. The students ___________ help the old woman clean the house.
2. I work hard ___________ those who care for me, help me and love me.
|
be
willing to; be active in ; blow up; in trouble; as a matter of fact |
1. I knew him when we were in college __________ we were on the same course.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com