
16.解:(Ⅰ)由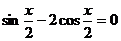 ,
, 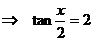 ,
………………………2分
,
………………………2分
 .
…………………5分
.
…………………5分
(Ⅱ) 原式= 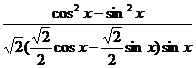 ……………………7分
……………………7分
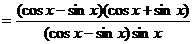 ………………………..9分
………………………..9分
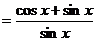 ……10分
……10分
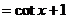
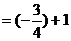
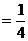 .
………………12分
.
………………12分
11.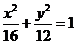 ;12.
;12.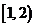 ; 13.
; 13. 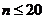 ; 14 .
; 14 .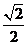 ;15.
;15.
21.(本小题满分14分)
定义域为R的偶函数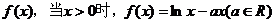 ,方程
,方程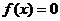 在R上恰有5个不同的实数解.
在R上恰有5个不同的实数解.
(Ⅰ)求x<0时,函数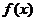 的解析式;
的解析式;
(Ⅱ)求实数a的取值范围.
20.(本题满分14分)
对于三次函数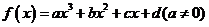 ,定义:设
,定义:设 是函数
是函数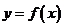 的导函数
的导函数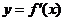 的导数,若
的导数,若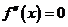 有实数解
有实数解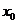 ,则称点
,则称点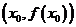 为函数
为函数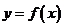 的“拐点”。现已知
的“拐点”。现已知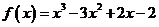 ,请解答下列问题:
,请解答下列问题:
(Ⅰ)求函数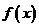 的“拐点”A的坐标;
的“拐点”A的坐标;
(Ⅱ)求证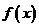 的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明);
的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明);
(Ⅲ)若另一个三次函数G(x)的“拐点”为B(0,1),且一次项系数为0,当 ,
,
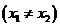 时,试比较
时,试比较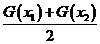 与
与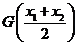 的大小。
的大小。
19.(本题满分14分)
设二次函数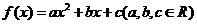 ,已知不论
,已知不论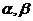 为何实数恒有
为何实数恒有
和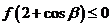 。
。
(Ⅰ)求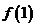 的值;
的值;
(Ⅱ)求证: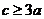 ;
;
(Ⅲ)若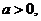 函数
函数 的最大值为8,求
的最大值为8,求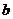 的值。
的值。
18.(本题满分14分)
某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度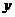 (米)随着时间
(米)随着时间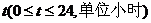 而周期性变化,每天各时刻
而周期性变化,每天各时刻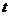 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
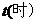 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 |
1.0 |
1.4 |
1.0 |
0.6 |
1.0 |
1.4 |
0.9 |
0.5 |
1.0 |
(Ⅰ)试画出散点图;
(Ⅱ)观察散点图,从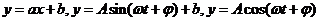 中选择一个合适的函数模型,并求出该拟合模型的解析式;
中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)如果确定在白天7时~19时当浪高不低于0。8米时才进行训练,试安排恰当的训练时间。
17.(本题满分(12分)
已知函数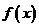 是定义在
是定义在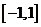 上的奇函数,在
上的奇函数,在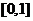 上
上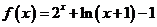
(Ⅰ)求函数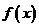 的解析式;并判断
的解析式;并判断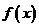 在
在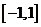 上的单调性(不要求证明)
上的单调性(不要求证明)
(Ⅱ)解不等式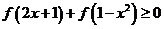 .
.
16.(本题满分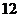 分)
分)
已知 ,
,
(Ⅰ)求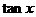 的值;
的值;
(Ⅱ)求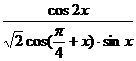 的值.
的值.
15、 (平面几何选讲选做题)如图,⊙
(平面几何选讲选做题)如图,⊙ 的割线
的割线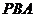 过圆心
过圆心 ,弦
,弦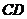 交
交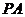 于点
于点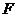 ,且△
,且△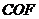 ∽△
∽△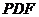 ,
,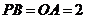 ,则
,则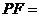 .
.
14、(坐标系与参数方程选做题)已知直线的极坐标方程为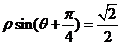 ,则极点到这条直线的距离是 .
,则极点到这条直线的距离是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com