
3.注意平行向量与平行线段的区别.用向量方法证明AB∥CD,需证 ∥
∥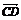 ,且AB与CD不共线.要证A、B、C三点共线,则证
,且AB与CD不共线.要证A、B、C三点共线,则证 ∥
∥ 即可.
即可.
2.注意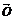 与O的区别.零向量与任一向量平行.
与O的区别.零向量与任一向量平行.
1.认识向量的几何特性.对于向量问题一定要结合图形进行研究.向量方法可以解决几何中的证明.
4.⑴ 平面向量基本定理:如果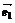 、
、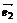 是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量
是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量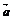 ,有且只有一对实数
,有且只有一对实数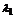 、
、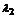 ,使得 .
,使得 .
⑵ 设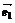 、
、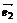 是一组基底,
是一组基底,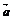 =
= ,
,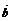 =
=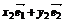 ,则
,则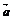 与
与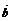 共线的充要条件是 .
共线的充要条件是 .
|
例1.已知△ABC中,D为BC的中点,E为AD的中点.设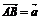 ,
,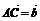 ,求
,求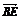 .
.
解: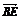 =
=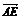 -
- =
=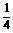 (
( +
+ )-
)- =-
=-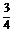
 +
+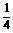
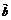
变式训练1.如图所示,D是△ABC边AB上的中点,则向量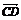 等于( )
等于( )
 A.-
A.-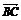 +
+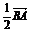
B.-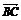 -
-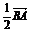
C.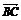 -
-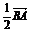
D.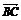 +
+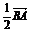
解:A
例2. 已知向量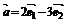 ,
,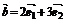 ,
,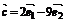 ,其中
,其中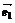 、
、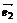 不共线,求实数
不共线,求实数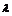 、
、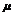 ,使
,使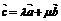 .
.
解: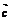 =λ
=λ +μ
+μ
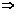 2
2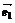 -9
-9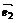 =(2λ+2μ)
=(2λ+2μ)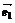 +(-3λ+3μ)
+(-3λ+3μ)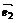
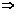 2λ+2μ=2,且-3λ+3μ=-9
2λ+2μ=2,且-3λ+3μ=-9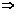 λ=2,且μ=-1
λ=2,且μ=-1
变式训练2:已知平行四边形ABCD的对角线相交于O点,点P为平面上任意一点,求证:
证明 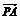 +
+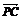 =2
=2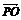 ,
,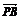 +
+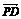 =2
=2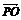
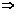
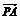 +
+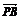 +
+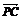 +
+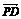 =4
=4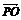
例3. 已知ABCD是一个梯形,AB、CD是梯形的两底边,且AB=2CD,M、N分别是DC和AB的中点,若 ,
, ,试用
,试用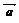 、
、 表示
表示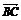 和
和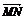 .
.
解:连NC,则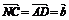
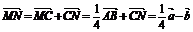 ;
;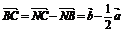
 变式训练3:如图所示,OADB是以向量
变式训练3:如图所示,OADB是以向量 =
= ,
, =
=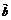 为邻边的平行四边形,又
为邻边的平行四边形,又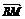 =
=
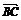 ,
,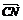 =
=
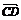 ,试用
,试用 、
、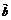 表示
表示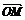 ,
,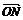 ,
, .
.
解: =
=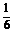
 +
+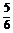
 ,
,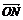 =
=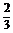
 +
+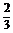
 ,
,
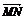 =
=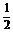
 -
-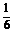

例4. 设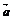 ,
,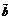 是两个不共线向量,若
是两个不共线向量,若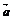 与
与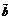 起点相同,t∈R,t为何值时,
起点相同,t∈R,t为何值时,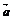 ,t
,t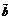 ,
, (
(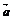 +
+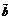 )三向量的终点在一条直线上?
)三向量的终点在一条直线上?
解:设 (
(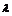 ∈R)化简整理得:
∈R)化简整理得: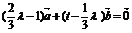
∵ ,∴
,∴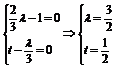
故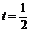 时,
时,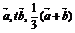 三向量的向量的终点在一直线上.
三向量的向量的终点在一直线上.
变式训练4:已知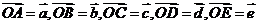 ,设
,设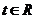 ,如果
,如果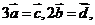
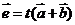 ,那么
,那么 为何值时,
为何值时,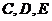 三点在一条直线上?
三点在一条直线上?
解:由题设知,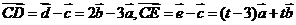 ,
,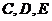 三点在一条
三点在一条
直线上的充要条件是存在实数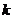 ,使得
,使得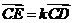 ,即
,即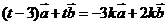 ,
,
整理得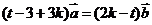 .
.
①若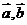 共线,则
共线,则 可为任意实数;
可为任意实数;
②若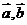 不共线,则有
不共线,则有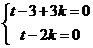 ,解之得,
,解之得,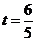 .
.
综上,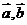 共线时,则
共线时,则 可为任意实数;
可为任意实数;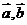 不共线时,
不共线时,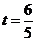 .
.
|
3.实数与向量的积
⑴ 实数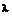 与向量
与向量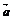 的积是一个向量,记作
的积是一个向量,记作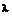
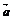 .它的长度与方向规定如下:
.它的长度与方向规定如下:
① | 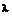
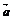 |=
.
|=
.
② 当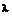 >0时,
>0时,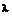
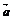 的方向与
的方向与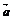 的方向 ;
的方向 ;
当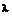 <0时,
<0时,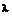
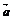 的方向与
的方向与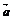 的方向 ;
的方向 ;
当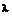 =0时,
=0时,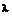
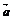 .
.
⑵ 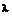 (μ
(μ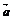 )=
.
)=
.
(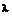 +μ)
+μ)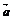 =
.
=
.
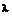 (
(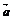 +
+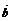 )=
.
)=
.
⑶ 共线定理:向量 与非零向量
与非零向量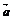 共线的充要条件是有且只有一个实数λ使得
.
共线的充要条件是有且只有一个实数λ使得
.
2.向量的加法与减法
⑴ 求两个向量的和的运算,叫向量的加法.向量加法按 法则或 法则进行.加法满足 律和 律.
⑵ 求两个向量差的运算,叫向量的减法.作法是将两向量的 重合,连结两向量的 ,方向指向 .
1.向量的有关概念
⑴ 既有 又有 的量叫向量.
的向量叫零向量. 的向量,叫单位向量.
⑵ 叫平行向量,也叫共线向量.规定零向量与任一向量 .
⑶ 且 的向量叫相等向量.
4.正弦定理、余弦定理及利用三角公式进行恒等变形的能力.以化简、求值或判断三角形的形状为主.解三角形常常作为解题工具用于立体几何中的计算或证明.
第1课时 向量的概念与几何运算
|
3.向量和其它数学知识的结合.如和三角函数、数列、曲线方程等及向量在物理中的应用.
2.向量的坐标运算及应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com