
337. 在平行六面体中,一个顶点上三条棱长分别是a,b,c,这三条棱长分别是a,b,c,这三条棱中每两条成60°角,求平行六面体积.
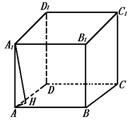
解析:如图,设过A点的三条棱AB,AD,AA1的长分别是a,b,c,且两面所成角是60°,过A1作A1H⊥平面ABCD,H为垂足,连HA,则∠HAB=30°,由课本题得:
cos∠A1AB=cos∠A1AH·cos∠HAB,
∴cos∠A1AH=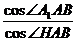 =
=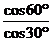 =
=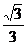 ,sin∠A1AH=
,sin∠A1AH=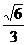
∴V=SABCD·A1H=absin60°·c·sin∠A1AH=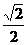 abc.
abc.
336. 在三棱柱ABC-A1B1C1中,已知AB=AC=10cm,BC=12cm,顶点A1与A、B、C的距离等于13cm,求这棱柱的全面积.
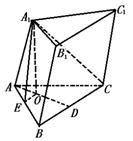
解析:如图,作A1O⊥平面ABC于O,∵A1A=A1B=A1C,∴OA=OB=OC,∴O是ΔABC的外心,∵ΔABC等腰,∴AO⊥BC于D,∴AA1⊥BC,∴B1B⊥BC,四边形B1BCC1为矩形,∴S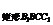 =12·13=156(cm2),ΔA1AB底边上高A1E=
=12·13=156(cm2),ΔA1AB底边上高A1E=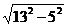 =12,
=12,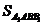 =
=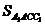 =120(cm2),SΔABC=
=120(cm2),SΔABC=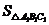 =
=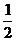 ·12·8=48(cm2),S全=156+2·120+2×48=492(cm2)
·12·8=48(cm2),S全=156+2·120+2×48=492(cm2)
335. 长方体的一条对角线与一个顶点上的三条棱所成的角分别为α、β、γ.
求证:cos2α+cos2β+cos2γ=1
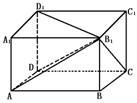
解析:证明三角恒等式,可用从左边推出右边的方法.
证明:设对角线B1D与长方体的棱AD、DC、D1D所成的角分别为α、β、γ,连结AB1、CB1,D1B1,则ΔB1DA、ΔB1DC、ΔB1DD1都是直角三角形.
∵cosα=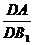 ,cosβ=
,cosβ=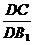 ,cosγ=
,cosγ=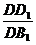
∴cos2α+cos2β+cos2γ=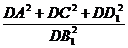 =1.
=1.
评析:这里运用了长方体对角线长定理.
334. (1)棱柱成为直棱柱的一个必要但不充分的条件是:( )
A.棱柱有一条侧棱与底面垂直
B.棱柱有一条侧棱与底面的两条边垂直
C.棱柱有两个相邻的侧面互相垂直
D.棱柱有一个侧面与底面的一条边垂直
解析: 根据直棱柱定义,A是充分条件,C、D不是必要条件,所以选B.
说明 解答此题要熟知直棱柱的定义及其充分必要条件的含义.
333. 一根长为a的木梁,它的两端悬挂在两条互相平行的,长度都为b的绳索下,木梁处于水平位置,如果把木梁绕通过它的中点的铅垂轴转动一个角度φ,那么木梁升高多少?
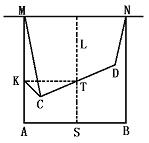
解析: 设M、N为悬挂点,AB为木梁的初始位置,那么AB=a,MA∥NB,MA=NB=b,∠A=∠B=90°.
设S为中点,L为过S的铅垂轴,那么L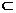 平面MANB,木梁绕L转动角度φ后位于CD位置,T为CD中点,那么木梁上升的高度为异面直线AB与CD之间的距离ST.
平面MANB,木梁绕L转动角度φ后位于CD位置,T为CD中点,那么木梁上升的高度为异面直线AB与CD之间的距离ST.
在平面MANB中,作TK∥AB,交MA于K,则AK=ST.
设ST=x,则x=b-KM.又KT=CT=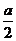 ,∠KTC=φ,有KC=asin
,∠KTC=φ,有KC=asin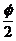 .
.
从而KM=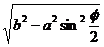 .
.
∴x=b-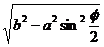 .
.
332. 三个平面两两相交得三条交线,若有两条相交,则第三条必过交点;若有两条平行,则第三条必与之平行.
已知:α∩β=a,α∩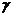 =b,
=b, 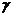 ∩α=c.
∩α=c.
求证:要么a、b、c三线共点,要么a∥b∥c.
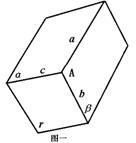
证明:①如图一,设a∩b=A,
∵α∩β=a.
∴a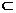 α而A∈a.
α而A∈a.
∴A∈α.
又β∩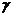 =b
=b
∴b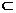
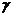 ,而A∈b.
,而A∈b.
∴A∈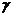 .
.
则A∈α,A∈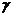 ,那么A在α、
,那么A在α、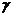 的交线c上.
的交线c上.
从而a、b、c三线共点.
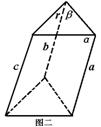
②如图二,若a∥b,显然c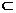
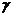 ,b
,b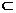
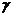
∴
a∥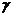
而
a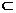 α, α∩
α, α∩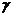 =c.
=c.
∴ a∥c
从而 a∥b∥c
331. 设a、b是两条异面直线,在下列命题中正确的是( )
A.有且仅有一条直线与a、b都垂直
B.有一平面与a、b都垂直
C.过直线a有且仅有一平面与b平行
D.过空间中任一点必可作一条直线与a、b都相交
解析: 因为与异面直线a、b的公垂线平行的直线有无数条,所以A不对;若有平面与a、b都垂直,则a∥b不可能,所以B不对.若空间的一点与直线a(或b)确定的平面与另一条直线b(或a)平行,则过点与a相交的直线必在这个平面内,它不可能再与另一条直线相交,所以D不对,故选C.
330. 在下列命题中,真命题是( )
A.若直线m、n都平行平面α,则m∥n;
B.设α-l-β是直二面角,若直线m⊥l,则m⊥n,m⊥β;
C.若直线m、n在平面α内的射影是一个点和一条直线,且m⊥n,则n在α内或n与α平行;
D.设m、n是异面直线,若m和平面α平行,则n与α相交.
解析:对于直线的平行有传递性,而两直线与平面的平行没有传递性故A不正确;平面与平面垂直可得出线面垂直,要一直线在一平面内且垂直于交线,而B中m不一定在α内,故不正确;对D来说存在平面同时和两异面直线平行,故不正确;应选C.
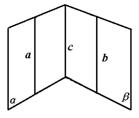
329.求证:如果两个相交平面分别经过两条平行直线中的一条,那么它们的交线和这条直线平行.
已知:a∥b,a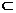 α,b
α,b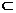 β,α∩β=c.
β,α∩β=c.
求证:c∥a∥b
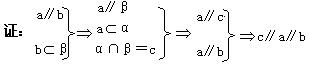
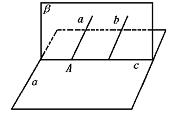
328.求证:如果两条平行线中的一条和一个平面相交,那么另一条也和这个平面相交.
已知:a∥b,a∩α=A,求证:b和α相交.
证明:假设b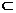 α或b∥α.
α或b∥α.
若b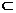 α,∵b∥a,∴a∥α.
α,∵b∥a,∴a∥α.
这与a∩α=A矛盾,∴b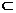 α不成立.
α不成立.
若b∥α,设过a、b的平面与α交于c.
∵b∥α,∴b∥c,又a∥b ∴a∥c
∴a∥α这与a∩α=A矛盾.∴b∥α不成立.
∴b与α相交.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com