
347. 线段AB长为2a,两端点A、B分别在一个直二面角的两个面上,AB和两个面所成的角为45°和30°,那么A、B在棱上的射影间的距离为( ).
A.2a
B.a
C.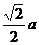 D.
D.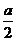
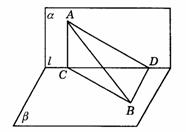
解析:B.如图答9-39,设直二面角为a -l-b ,作AC⊥l于C,BD⊥l于D,则AC⊥b ,BD⊥a ,连结AD、BC,∴ ∠ABC为AB与b 所成的角,∠BAD为AB与a 所成的角,∴
∠ABC=30°,∠BAD=45°,∵ AB=2a,∴ AC=a,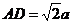 .在Rt△ACD中,
.在Rt△ACD中,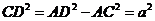 ,∴ CD=a.
,∴ CD=a.
图答9-39
346.
SA、SB、SC是从S点出发的三条射线,若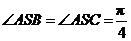 ,
,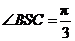 ,则
,则
二面角B-SA-C的大小为( ).
A.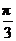 B.
B.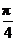 C.
C.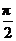 D.
D.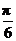
解析:C.在SA上任取一点E,作EF⊥SA交SC于F,作EG⊥SA交SB于G,连结FG,则∠GEF为二面角B-SA-C的平面角.
345.
如图9-45,二面角a
-l-b 的平向角为120°,A∈l,B∈l,AC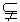 a ,BD
a ,BD b ,AC⊥l,BD⊥l.若AB=AC=BD=1,则CD长为( ).
b ,AC⊥l,BD⊥l.若AB=AC=BD=1,则CD长为( ).
A.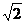 B.
B.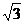 C.2
D.
C.2
D.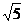
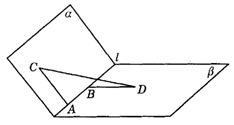
解析:B.在平面b
内作AE∥BD,DE∥BA,得交点E.则∠CAE为二面角a -l-b 的平面角,故∠CAE=120°,于是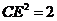 .在Rt△CED中可求CD长.
.在Rt△CED中可求CD长.
344.
直线l、m与平面a 、b
满足l⊥平面a
,m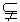 b ,以上四个命题:
b ,以上四个命题:
①a ∥b 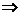 l ⊥m;②a
⊥b
l ⊥m;②a
⊥b 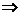 l∥m;③l∥m
l∥m;③l∥m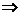 a ⊥b
;④l⊥m
a ⊥b
;④l⊥m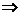 a ∥b .
a ∥b .
其中正确的两个命题是( ).
A.①与② B.③与④ C.②与④ D.①与③
解析:D.

343.
已知a -l-b
是直二面角,直线a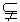 a ,直线b
a ,直线b b ,且a、b与l都不垂直,那么( ).
b ,且a、b与l都不垂直,那么( ).
A.a与b可能平行,也可能垂直
B.a与b可能平行,但不可能垂直
C.a 与b不可能平行,但可能垂直
D.a 与b不可能平行,也不可能垂直
解析:B.当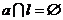 ,
,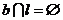 时,a∥b,即a、b可能平行,假设a⊥b,在a上取一点P,作PQ⊥l交l于Q,∵ 二面角a -l-b 是直二面角,∴ PQ⊥b ,∴ PQ⊥b.∴ b垂直于a 内两条相交直线a和PQ,∴ b⊥a ,∴ b⊥l.这与已知b与l不垂直矛盾.∴ b与a不垂直
时,a∥b,即a、b可能平行,假设a⊥b,在a上取一点P,作PQ⊥l交l于Q,∵ 二面角a -l-b 是直二面角,∴ PQ⊥b ,∴ PQ⊥b.∴ b垂直于a 内两条相交直线a和PQ,∴ b⊥a ,∴ b⊥l.这与已知b与l不垂直矛盾.∴ b与a不垂直
342. 已知异面直线a、b成角,过空间一点p,与a、b也都成角的直线,可以作( )
A.1条 B.2条 C.3条 D.4条
解析:C
341. 在三棱柱ABC-A1B1C1中,AB=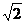 a,BA=CA=AA1=a,A1在底面ΔABC上的射影O在AC上。
a,BA=CA=AA1=a,A1在底面ΔABC上的射影O在AC上。
(1)求AB与侧面AC1所成的角
(2)若O恰是AC的中点,求此三棱柱的侧面积
解析: (1)A1O⊥面ABC,BC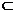 面ABC,∴BC⊥A1O,又∵BC=CA=a,AB=
面ABC,∴BC⊥A1O,又∵BC=CA=a,AB=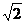 a,∴ΔABC是等腰直角三角形,∴BC⊥AC,∵BC⊥面AC1,故∠BAC为BA与面AC1所成的角,则有∠BAC= 45°,即AB与侧面成45°角。
a,∴ΔABC是等腰直角三角形,∴BC⊥AC,∵BC⊥面AC1,故∠BAC为BA与面AC1所成的角,则有∠BAC= 45°,即AB与侧面成45°角。
(2)若O恰为AC中点,∵AA1=a,AC=a,∴AO=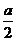 ,A1O=
,A1O=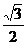 a,
a,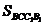 =a2,作OD⊥AB于D,连结A1D,由三垂线定理得A1D⊥AB,在RtΔAOD中,OD=OAsin∠BAC=
=a2,作OD⊥AB于D,连结A1D,由三垂线定理得A1D⊥AB,在RtΔAOD中,OD=OAsin∠BAC=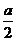 ·
·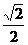 =
=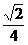 a2,在RtΔA1OD中,A1D=
a2,在RtΔA1OD中,A1D=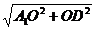 =
=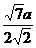 ,
,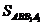 =
=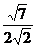 a·
a·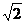 ·a=
·a=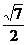 a2,∴
a2,∴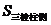 =
=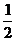 (2+
(2+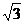 +
+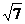 )a2
)a2
340. 如图,已知正三棱柱A1B1C1-ABC的底面积等于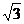 cm2,D、E分别是侧棱B1B,C1C上的点,且有EC=BC=2DB,试求
cm2,D、E分别是侧棱B1B,C1C上的点,且有EC=BC=2DB,试求
(1)四棱锥A-BCDE的底面BCED的面积
(2)四棱锥A-BCED的体积
(3)截面ADE与底面ABC所成二面角的大小
(4)截面ADE的面积
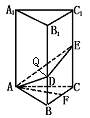
解析: 利用三棱柱的性质及已知条件,(1)、(2)、(4)不难推算,至于(3),可设平面ADE与平面ABC所成二面角为α,观察到ΔADE在底面ABC的射影是ΔABC(∵DB⊥平面ABC,EC⊥平面ABC)应用SΔABC=SΔADE·cosα,可求出α.
解:设ΔABC边长为x,∵SΔABC=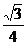 x2=
x2=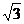 .∴x=2,于是EC=BC=2,DB=
.∴x=2,于是EC=BC=2,DB=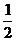 BC=1,∴SBCED=
BC=1,∴SBCED=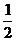 (2+1)·2=3,作AF⊥BC于F
(2+1)·2=3,作AF⊥BC于F
∴AF⊥平面BCED,VA-BCED=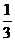 ·AF·SBCED,∴VA-BCED=
·AF·SBCED,∴VA-BCED=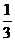 ·
·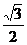 ·2·3=
·2·3=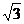
在RtΔABD中,AD2=AB2+DB2=22+12=5;在Rt梯形BCED中,DE2=(CE-DB)2+BC2=5
∴AD=DE=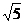 ,∴ΔADE是等腰三角形,作DQ⊥AE于Q,则Q为AE的中点
,∴ΔADE是等腰三角形,作DQ⊥AE于Q,则Q为AE的中点
在RtΔACE中,AE2=EC2+AC2=8,DQ2=AD2-AQ2=(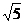 )2-(
)2-(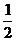
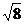 )2=3
)2=3
∴AE=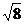 ,DQ=
,DQ=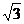 ,SΔADE=
,SΔADE=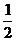 ·AE·DQ=
·AE·DQ=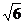
设截面ADE与底面ABC所成二面角大小为α,D、E分别在底面的射影为B、C,∴ΔABC的面积=ΔADE面积×cosα
即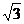 =
=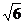 cosα,cosα=
cosα,cosα=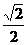 ,∴α=45°
,∴α=45°
答
(1)SBCED=3cm2,(2)VA-BCED=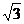 cm2,(3)截面ADE与底面ABC成45°的二面角,(4)SΔADE=
cm2,(3)截面ADE与底面ABC成45°的二面角,(4)SΔADE=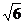 cm2
cm2
339. 如图,已知正三棱柱ABC-A1B1C1的各棱长都为a,D为CC1的中点.
(1)求证:A1B⊥平面AB1D.
(2)求平面A1BD与平面ABC所成二面角的度数.
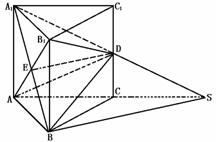
解析:这虽是一个棱柱,但所要论证的线面关系以及二面角的度数,都还是要利用直线和平面中的有关知识.
解 (1)∵正三棱柱的各棱长都相等,
∴侧面ABB1A1是正方形.
∴A1B⊥AB1.连DE,
∵ΔBCD≌ΔA1C1D,
∴BD=A1D,而E为A1B的中点,
A1B⊥DE.∴A1B⊥平面AB1D.
(2)延长A1D与AC的延长线交于S,连BS,则BS为平面A1BD和平面ABC所成二面角的公共棱.
∵DC∥A1A,且D为CC1的中点,∴AC=CS.
又AB=BC=CA=CS,∴∠ABS=90°.又AB是A1B在底面上的射影,由三垂线定理得A1B⊥BS.
∴∠A1BA就是二面角A1-BS-A的平面角.
∵∠A1BA=45°,
∴平面A1BD和平面ABC所成的二面角为45°.
评注:本题(2)的关键是根据公理二求平面A1BD和平面ABC的交线,在论证AB⊥BS时,用到了直角三角形斜边上的中线性质定理的逆定理.当然(2)还可以用S射=S·cosθ来解θ.
338. 在棱长为a的正三棱柱ABC-A1B1C1中,O、O1分别为两底中心,P为OO1的中点,过P、B1、C1作一平面与此三棱柱相截,求此截面面积.
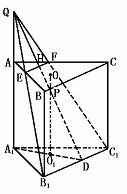
解析: 如图,∵AA1⊥面A1B1C1,AA1∥OO1,设过P、B1、C1的截面与AA1的延长线交于Q,连结A1O1延长交B1C1于D,连QD,则P必在QD上,∵O1为ΔA1B1C1的中心,P为OO1的中点,故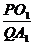 =
=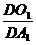 =
=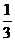 ,∴Q在A1A延长线上且QA=PO1,又QB1交AB于E,QC1交AC于F,则EF∥B1C1,所以截面为EFB1C1是等腰梯形,又QA1∶QA=3∶1,∴EF=
,∴Q在A1A延长线上且QA=PO1,又QB1交AB于E,QC1交AC于F,则EF∥B1C1,所以截面为EFB1C1是等腰梯形,又QA1∶QA=3∶1,∴EF=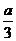 设QD与EF交于H,得QD⊥B1C1.因此HD为梯形EFC1B1的高.DQ=
设QD与EF交于H,得QD⊥B1C1.因此HD为梯形EFC1B1的高.DQ=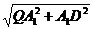 =
=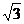 a,∴HD=
a,∴HD=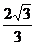 a.
a.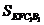 =
=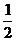 (a+
(a+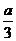 )·(
)·(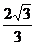 a)=
a)=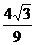 a2为所求截面积.
a2为所求截面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com