
129. 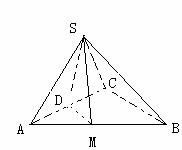 如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=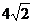 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。
解析:先作出二面角的平面角。由面面垂直可得线面垂直,作SD⊥平面ACB,然后利用三垂线定理作出二面角的平面角
解:过S点作SD⊥AC于D,过D作DM⊥AB于M,连SM
∵平面SAC⊥平面ACB
∴SD⊥平面ACB
∴SM⊥AB
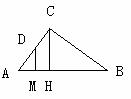 又∵DM⊥AB
又∵DM⊥AB
∴∠DMS为二面角S-AB-C的平面角
在ΔSAC中SD=4×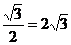
在ΔACB中过C作CH⊥AB于H
∵AC=4,BC=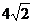
∴AB=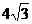
∵S=1/2AB·CH=1/2AC·BC
∴CH=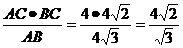
∵DM∥CH且AD=DC
∴DM=1/2CH=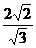
∵SD⊥平面ACB DMÌ平面ACB
∴SD⊥DM
在RTΔSDM中
SM=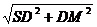
=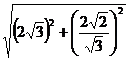
=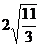
∴cos∠DMS=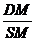
=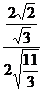
=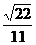
128. 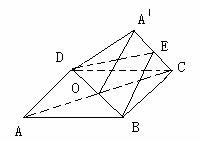 正方形ABCD中,以对角线BD为折线,把ΔABD折起,使二面角Aˊ-BD-C 为60°,求二面角B-AˊC-D的余弦值
正方形ABCD中,以对角线BD为折线,把ΔABD折起,使二面角Aˊ-BD-C 为60°,求二面角B-AˊC-D的余弦值
解析:要求二面角B-AˊC-D的余弦值,先作出二面角的平面角,抓住图形中AˊB=BC,AˊD=DC的关系,采用定义法作出平面角∠BED(E为AC的中点)然后利用余弦定理求解
解:连BD、AC交于O点
则AˊO⊥BD,CO⊥BD
∴∠AˊOC为二面角Aˊ-BD-C的平面角
∴∠AˊOC=60°
设正方形ABCD的边长为a
∵A′O=OC=1/2AC=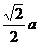
∠A′OC=60°
∴ΔA′OC为正三角形则A′C=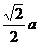
取A′C的中点,连DE、BE
∵A′B=BC
∴BE⊥A′C
同理DE⊥A′C
∴∠DEB为二面角B-A′C-D的平面角在ΔBA′C中
BE=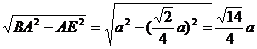
同理DE=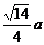
在ΔBED中,BD=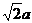
∴ cos∠BED=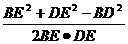
=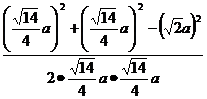
=--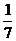
∴二面角B-A′C-D的余弦值为-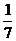
127. 已知空间四边形ABCD中,AB = BC =CD= AD = BD = AC, E、F分别为AB、CD的中点,
(1)求证:EF 为AB和CD的公垂线
(2)求异面直线AB和CD的距离
解析:构造等腰三角形证明EF 与AB、CD垂直,然后在等腰三角形中求EF
解;①连接BD和AC,AF和BF,DE和CE
设四边形的边长为a
∵ AD = CD = AC = a
∴ △ABC为正三角形
∵ DF = FC
∴ AF ^ DC 且AF =
同理 BF = A
即△ AFB为等腰三角形
在△ AFB中,
∵ AE = BE
∴ FE ^ AB
同理在 △ DEC中
EF ^ DC
∴ EF为异面直线AB和CD的公垂线
②在 △ AFB中
∵ EF ^ AB且 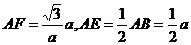
∴ 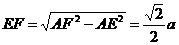
∵ 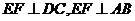
∴ EF为异面直线AB和CD的距离
∴ AB和CD的距离为
126.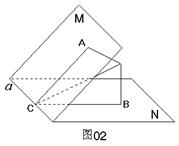 在60°的二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求P点到直线a的距离.
在60°的二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求P点到直线a的距离.
解析:本题涉及点到平面的距离,点到直线的距离,二面角的平面角等概念,图中都没有表示,按怎样的顺序先后作出相应的图形是解决本题的关键.可以有不同的作法,下面仅以一个作法为例,说明这些概念的特点,分别作PA⊥M,M是垂足,PB⊥N,N是垂足,先作了两条垂线,找出P点到两个平面的距离,其余概念要通过推理得出:于是PA、PB确定平面α,设α∩M=AC,α∩N=BC,c∈a.由于PA⊥M,则PA⊥a,同理PB⊥a,因此a⊥平面α,得a⊥PC.这样,∠ACB是二面角的平面角,PC是P点到直线a的距离,下面只要在四边形ACBP内,利用平面几何的知识在△PAB中求出AB,再在△ABC中利用正弦定理求外接圆直径2R=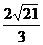 ,即为P点到直线a的距离,为
,即为P点到直线a的距离,为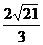 .
.
125. 如图,正方体ABCD-A1B1C1D1中,E、F分别为AB、CC1的中点,则异面直线A1C与EF所成角的余弦值是 ( )
(A) 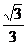 (B)
(B)
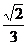 (C)
(C)
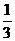 (D)
(D)
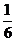
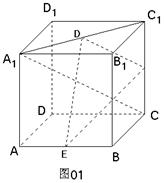 解析:选哪一点,如何作平行线是解决本题的关键,显然在EF上选一点作AC的平行线要简单易行,观察图形,看出F与A1C确定的平面A1CC1恰是正方体的对角面,在这个面内,只要找出A1C1的中点O,连结OF,这条平行线就作出了,这样,∠EFO即为异面直线A1C与EF所成的角.容易算出这个角的余弦值是
解析:选哪一点,如何作平行线是解决本题的关键,显然在EF上选一点作AC的平行线要简单易行,观察图形,看出F与A1C确定的平面A1CC1恰是正方体的对角面,在这个面内,只要找出A1C1的中点O,连结OF,这条平行线就作出了,这样,∠EFO即为异面直线A1C与EF所成的角.容易算出这个角的余弦值是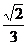 ,答案选B.
,答案选B.
124. 二面角α-a-β是120°的二面角,P是该角内的一点.P到α、β的距离分别为a,b.求:P到棱a的距离.
解析:设PA⊥α于A,PB⊥β于B.过PA与PB作平面r与α交于AO,与β交于OB,
∵ PA⊥α,PB⊥β,∴ a⊥PA,且a⊥PB
∴ a⊥面r,∴ a⊥PO,PO的长为P到棱a的距离.
且∠AOB是二面角之平面角,∠AOB =120°
∴ ∠APB = 60°,PA = a,PB = b.
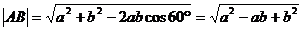
∵ 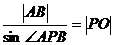 ,
,
∴ 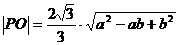 .
.
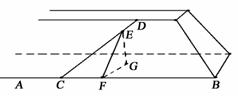
123. 河堤斜面与水平面所成角为60°,堤面上有一条直道CD,它与堤角的水平线AB的夹角为30°,沿着这条直道从堤角向上行走到10米时,人升高了多少(精确到0.1米)?
解析: 已知 所求
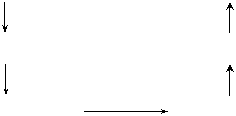
河堤斜面与水平面所成角为60° E到地面的距离
利用E或G构造棱上一点F 以EG为边构造三角形
解:取CD上一点E,设CE=10 m,过点E作直线AB所在的水平面的垂线EG,垂足为G,则线段EG的长就是所求的高度.
在河堤斜面内,作EF⊥AB.垂足为F,连接FG,由三垂线定理的逆定理,知FG⊥AB.因此,∠EFG就是河堤斜面与水平面ABG所成的二面角的平面角,∠EFG=60°.
 由此得:
由此得:
EG=EFsin60°
=CE sin30°sin60°
=10×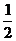 ×
×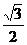 ≈4.3(m)
≈4.3(m)
答:沿着直道向上行走到10米时,人升高了约4.3米.
122. 在四面体ABCD中,AB=AD=BD=2,BC=DC=4,二面角A-BD-C的大小为60°,求AC的长.
解析:作出二面角A-BD-C的平面角
在棱BD上选取恰当的点
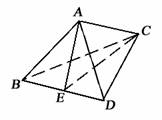 AB=AD,BC=DC
AB=AD,BC=DC
解:取BD中点E,连结AE,EC
∵ AB=AD,BC=DC
∴ AE⊥BD,EC⊥BD
∴ ∠AEC为二面角A-BD-C的平面角
∴ ∠AEC=60°
∵ AD=2,DC=4
∴ AE=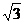 ,EC=
,EC=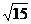
∴ 据余弦定理得:AC=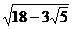 .
.
121. 已知:如图12,P是正方形ABCD所在平面外一点,PA=PB=PC=PD=a,AB=a.
求:平面APB与平面CPD相交所成较大的二面角的余弦值.

分析:为了找到二面角及其平面角,必须依据题目的条件,找出两个平面的交线.
解:因为 AB∥CD,CD 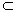 平面CPD,AB
平面CPD,AB  平面CPD.
平面CPD.
所以 AB∥平面CPD.
又 P∈平面APB,且P∈平面CPD,
因此 平面APB∩平面CPD=l,且P∈l.
所以 二面角B-l-C就是平面APB和平面CPD相交所得到的一个二面角.
因为 AB∥平面CPD,AB  平面APB,平面CPD∩平面APB=l,
平面APB,平面CPD∩平面APB=l,
所以 AB∥l.
过P作PE⊥AB,PE⊥CD.
因为 l∥AB∥CD,
因此 PE⊥l,PF⊥l,
所以 ∠EPF是二面角B-l-C的平面角.
因为 PE是正三角形APB的一条高线,且AB=a,
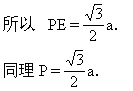
因为 E,F分别是AB,CD的中点,
所以 EF=BC=a.
在△EFP中,
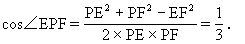

120. 如图, 在空间四边形SABC中, SA^平面ABC, ÐABC = 90°, AN^SB于N, AM^SC于M。求证: ①AN^BC; ②SC^平面ANM
解析: ①要证AN^BC, 转证, BC^平面SAB。
②要证SC^平面ANM, 转证, SC垂直于平面ANM内的两条相交直线, 即证SC^AM, SC^AN。要证SC^AN, 转证AN^平面SBC, 就可以了。
证明:
①∵SA^平面ABC
∴SA^BC
又∵BC^AB, 且ABSA = A
∴BC^平面SAB
∵AN平面SAB
∴AN^BC
②∵AN^BC, AN^SB, 且SBBC = B
∴AN^平面SBC
∵SCC平面SBC
∴AN^SC
又∵AM^SC, 且AMAN = A
∴SC^平面ANM
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com