
73、(江苏省南通通州市2008届高三年级第二次统一测试)函数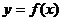 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数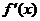 是减函数,且
是减函数,且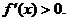 设
设 是曲线
是曲线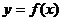 在点(
在点( )处的切线方程,并设函数
)处的切线方程,并设函数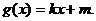
(1)用 、
、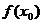 、
、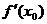 表示m;
表示m;
(2)证明:当 ;
;
(3)是否存在实数a,使得若关于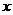 的不等式
的不等式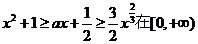 上恒成立?若存在,求出a的范围,若不存在说明理由。
上恒成立?若存在,求出a的范围,若不存在说明理由。
解:(1)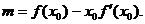 5′
5′
(2)证明:令
因为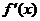 递减,所以
递减,所以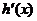 递增,因此,当
递增,因此,当 ;
;
当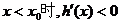 .所以
.所以 是
是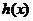 唯一的极值点,且是极小值点,可知
唯一的极值点,且是极小值点,可知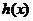 的
的
最小值为0,因此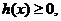 即
即 11′
11′
(3)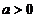 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.
 对任意
对任意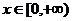 成立的充要条件是
成立的充要条件是
 14′
14′
令 ,于是
,于是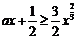 对任意
对任意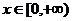 成立的充要条件是
成立的充要条件是
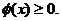 由
由
当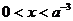 时
时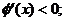 当
当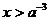 时,
时, ,所以,当
,所以,当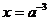 时,
时,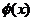 取最小值.因此
取最小值.因此 成立的充要条件是
成立的充要条件是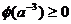 ,即
,即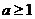 17′
17′
综上所述,当1≤a≤ 不等式
不等式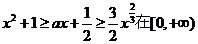 成立. 18′
成立. 18′
72、(江苏省泰兴市2007-2008学年第一学期高三调研)设常数 ,函数
,函数
 .
.
(1)令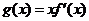
 ,求
,求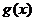 的最小值,并比较
的最小值,并比较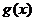 的最小值与零的大小;
的最小值与零的大小;
(2)求证: 在
在 上是增函数;
上是增函数;
(3)求证:当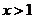 时,恒有
时,恒有 .
.
解(Ⅰ)∵ ,
,
∴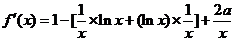 ,
,
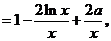 ……2分
……2分
∴ ,
,
∴ ,令
,令 ,得
,得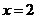 ,
……4分
,
……4分
列表如下:
|
x |
(0,2) |
2 |
(2,+∞) |
|
g'(x) |
- |
0 |
+ |
|
g(x) |
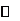 |
极小值g(2) |
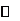 |
∴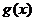 在
在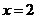 处取得极小值
处取得极小值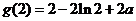 ,
,
即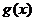 的最小值为
的最小值为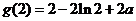 .
……6分
.
……6分
 ,
,
∵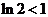 ,∴
,∴ ,又
,又 ,
,
∴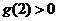 .
……8分
.
……8分
证明(Ⅱ)由(Ⅰ)知,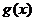 的最小值是正数,
的最小值是正数,
∴对一切 ,恒有
,恒有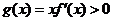 ,
……10分
,
……10分
从而当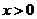 时,恒有
时,恒有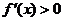 ,
……11分
,
……11分
故 在
在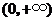 上是增函数.
……12分
上是增函数.
……12分
证明(Ⅲ)由(Ⅱ)知: 在
在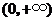 上是增函数,
上是增函数,
∴当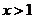 时,
时, ,
……13分
,
……13分
又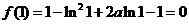 ,
……14分
,
……14分
∴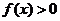 ,即
,即 ,
……15分
,
……15分
∴
故当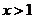 时,恒有
时,恒有 .
……16分
.
……16分
71、(江苏省前黄高级中学2008届高三调研)设三次函数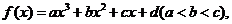 在
在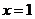 处取得极值,其图象在
处取得极值,其图象在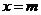 处的切线的斜率为
处的切线的斜率为 。
。
(Ⅰ)求证: ;
;
(Ⅱ)若函数 在区间
在区间 上单调递增,求
上单调递增,求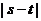 的取值范围;
的取值范围;
(Ⅲ)问是否存在实数 (
( 是与
是与 无关的常数),当
无关的常数),当 时,恒有
时,恒有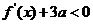 恒成立?若存在,试求出
恒成立?若存在,试求出 的最小值;若不存在,请说明理由。
的最小值;若不存在,请说明理由。
解:(Ⅰ)方法一、 .由题设,得
.由题设,得 ①
①
 ②
②
∵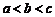 ,∴
,∴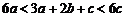 ,∴
,∴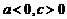 。
。
由①代入②得 ,∴
,∴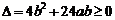 ,
,
得 ∴
∴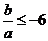 或
或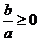 ③
③
将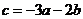 代入
代入 中,得
中,得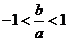 ④
④
由③、④得 ;
;
方法二、同上可得: 将(1)变为:
将(1)变为: 代入(2)可得:
代入(2)可得: ,所以
,所以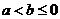 ,则
,则
方法三:同上可得: 将(1)变为:
将(1)变为: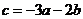 代入(2)可得:
代入(2)可得: ,显然
,显然 ,所以
,所以
因为 图象的开口向下,且有一根为x1=1
图象的开口向下,且有一根为x1=1
由韦达定理得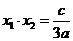 ,
,
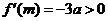 ,所以
,所以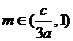 ,即
,即 ,则
,则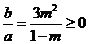 ,由
,由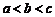 得:
得:
所以:
方法四:由 得:
得: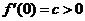 且
且 ,由此可知
,由此可知
(Ⅱ)由(1)知, 的判别式Δ=
的判别式Δ=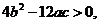
∴方程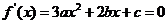 有两个不等的实根
有两个不等的实根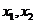 ,
,
又 ,∴
,∴ ,
,
∴当 或
或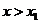 时,
时,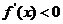 ,当
,当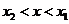 时,
时, ,
,
∴函数 的单调增区间是
的单调增区间是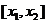 ,∴
,∴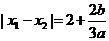 ,由
,由 知
知 。
。
∵函数 在区间
在区间 上单调递增,∴
上单调递增,∴ ,∴
,∴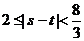 ,即
,即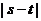 的取值范围是
的取值范围是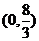 ;
;
(Ⅲ)由 ,即
,即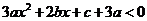 ,∵
,∵ ,
,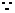
 ,∴
,∴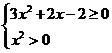 ,∴
,∴ 或
或 。由题意,得
。由题意,得 ,∴
,∴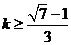 ,∴存在实数
,∴存在实数 满足条件,即
满足条件,即 的最小值为
的最小值为 。
。
70、(江苏省南通市2008届高三第二次调研考试)已知函数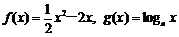 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果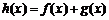 是增函数,且
是增函数,且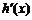 存在零点(
存在零点(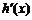 为
为 的导函数).
的导函数).
(Ⅰ)求a的值;
(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,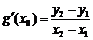 (
(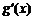 为
为 的导函数),证明:
的导函数),证明: .
.
解:(Ⅰ)因为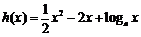
 ,
,
所以 . …………………………………………3分
. …………………………………………3分
因为h(x)在区间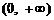 上是增函数,
上是增函数,
所以 在区间
在区间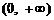 上恒成立.
上恒成立.
若0<a<1,则lna<0,于是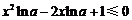 恒成立.
恒成立.
又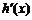 存在正零点,故△=(-2lna)2-4lna=0,lna=0,或lna=1与lna<0矛盾.
存在正零点,故△=(-2lna)2-4lna=0,lna=0,或lna=1与lna<0矛盾.
所以a>1.
由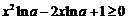 恒成立,又
恒成立,又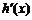 存在正零点,故△=(-2lna)2-4lna=0,
存在正零点,故△=(-2lna)2-4lna=0,
所以lna=1,即a=e. ……………………………………………………………………7分
(Ⅱ)由(Ⅰ), ,于是
,于是 ,
,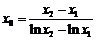 .…………………………9分
.…………………………9分
以下证明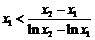 . (※)
. (※)
(※)等价于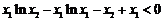 . ……………………………………………11分
. ……………………………………………11分
令r(x)=xlnx2-xlnx-x2+x,…………………………………………………………13分
r ′(x)=lnx2-lnx,在(0,x2]上,r′(x)>0,所以r(x)在(0,x2]上为增函数.
当x1<x2时,r(x1)< r(x2)=0,即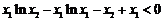 ,
,
从而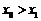 得到证明.……………………………………………………………………15分
得到证明.……………………………………………………………………15分
对于 同理可证……………………………………………………………16分
同理可证……………………………………………………………16分
所以 .
.
评讲建议:
此题主要考查函数、导数、对数函数、二次函数等知识.评讲时注意着重导数在研究函数中的应用.本题的第一小题是常规题比较容易,第二小题是以数学分析中的中值定理为背景,作辅助函数,利用导数来研究函数的性质,是近几年高考的热点.第二小题还可以这样证明:
要证明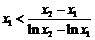 ,只要证明
,只要证明 >1,令
>1,令 ,作函数h(x)=t-1-lnt,下略.
,作函数h(x)=t-1-lnt,下略.
69、(江苏省常州市北郊中学2008届高三第一次模拟检测)已知函数
(1)求函数 的单调区间;
的单调区间;
(2)若 ≤0恒成立,试确定实数k的取值范围;
≤0恒成立,试确定实数k的取值范围;
(3)证明:
解:(1)函数 的定义域为(0,+
的定义域为(0,+ )
)
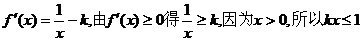 (2分)
(2分)
当k>0时,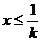 ,所以函数
,所以函数 的单调递增区间为(0,
的单调递增区间为(0,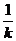 )单调递减区是为
)单调递减区是为
当k=0时,不等式恒成立,所以函数 是单调递增区间为(0,+
是单调递增区间为(0,+ )
)
当k<0时,因为x>0,所以不等式恒成立,所以函数 是单调递增区间为(0,+
是单调递增区间为(0,+ )
)
综上所述,当k>0时,函数 的单调递增区间为(0,
的单调递增区间为(0,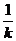 ),单调递减区间为[
),单调递减区间为[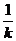 ,+
,+ );当k≤0时,函数
);当k≤0时,函数 的单调递增区间为(0,+
的单调递增区间为(0,+ )。(5分)
)。(5分)
(2)由(1)知k≤时,函数 是增函数,而
是增函数,而 ,不成立,所以k>0,由(1)可得
,不成立,所以k>0,由(1)可得 恒成立,只需
恒成立,只需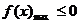 ,
,
所以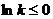 所以k≥1(9分)
所以k≥1(9分)
(3)由(2)可得当k=1时,lnx≤x-1在(0,+ )上恒成立。
)上恒成立。
ln2≤1 ln3≤2 ln4≤3 ……
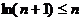 以上各式左右两边分别相加得
以上各式左右两边分别相加得
≤1+2+3+…+n=

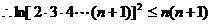
68、(吉林省实验中学2008届高三年级第五次模拟考试)已知函数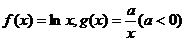 ,设
,设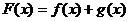 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以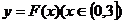 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率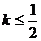 恒成立,求实数
恒成立,求实数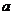 的最小值。
的最小值。
(Ⅲ)是否存在实数 ,使得函数
,使得函数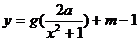 的图象与
的图象与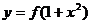 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说名理由。
的取值范围,若不存在,说名理由。
解.(Ⅰ) 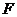



由 。
。
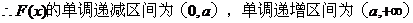
(Ⅱ)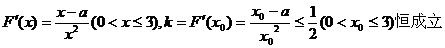
 当
当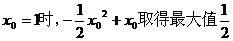
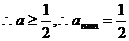 …………………………………………4分
…………………………………………4分
(Ⅲ)若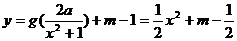 的图象与
的图象与
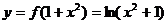 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即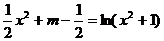 有四个不同的根,亦即
有四个不同的根,亦即
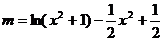 有四个不同的根。
有四个不同的根。
令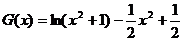 ,
,
则 。
。
当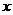 变化时
变化时 的变化情况如下表:
的变化情况如下表:
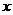 |
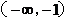 |
(-1,0) |
(0,1) |
(1,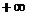 ) ) |
 的符号 的符号 |
+ |
- |
+ |
- |
 的单调性 的单调性 |
↗ |
↘ |
↗ |
↘ |
由表格知: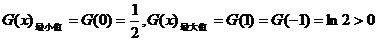 。
。
画出草图和验证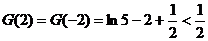 可知,当
可知,当 时,
时,


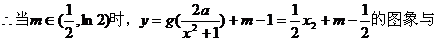
 ………………12分
………………12分
67、(黄家中学高08级十二月月考)设函数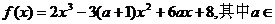 R.
R.
(1)若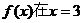 处取得极值,求常数a的值;
处取得极值,求常数a的值;
(2)若 上为增函数,求a的取值范围.
上为增函数,求a的取值范围.
[解]:(Ⅰ)
因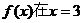 取得极值, 所以
取得极值, 所以 解得
解得
经检验知当 为极值点.
为极值点.
(Ⅱ)令
当
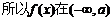 和
和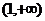 上为增函数,
上为增函数,
故当 上为增函数.
上为增函数.
当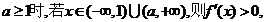
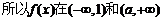 上为增函数,
上为增函数,
从而 上也为增函数.
上也为增函数.
综上所述,当 上为增函数.
上为增函数.
66、(湖南省岳阳市2008届高三第一次模拟)(1)已知函数m(x)=ax2e-x (a>0), 求证: 函数y=m(x)在区间[2,+∞)上为减函数.
(2) 已知函数f(x)=ax2+2ax, g(x)=ex, 若在(0, +∞)上至少存在一点x0, 使得f(x0)>g(x0)成立, 求实数a的取值范围.
解:(1) m '(x)= axe-x(2-x), 而ax>0, ∴当x>2时, m '(x)<0, 因此m(x)在[2,+∞)上为减函数.
(2)记m(x)=, 则m'(x)=(-ax2+2a)e-x,
当x>时, m '(x)<0 当0<x<时, m '(x)>0
故m(x)在x=时取最大值,同时也为最大值. m(x)max=m()=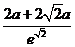
依题意, 要在(0,+∞)上存在一点x0, 使f(x0)>g(x0)成立. 即使m(x0)>1只需m()>1
即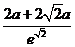 >1 ∴
>1 ∴ 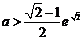 , 因此, 所求实数a的取值范围为(
, 因此, 所求实数a的取值范围为(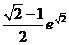 ,
+∞)
,
+∞)
65、(湖南省雅礼中学2008年高三年级第六次月考)已知函数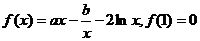 .
.
(Ⅰ)若函数f(x)在其定义域内为单调函数,求a的取值范围;
(Ⅱ)若函数f(x)的图象在x = 1处的切线的斜率为0,且 ,已知a1 = 4,求证:an ³ 2n + 2;
,已知a1 = 4,求证:an ³ 2n + 2;
(Ⅲ)在(Ⅱ)的条件下,试比较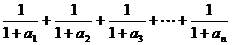 与
与 的大小,并说明你的理由.
的大小,并说明你的理由.
解:(1)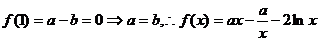 ,
, .
.
要使函数f(x)在定义域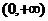 内为单调函数,则在
内为单调函数,则在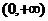 内
内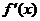 恒大于0或恒小于0,
恒大于0或恒小于0,
当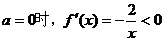 在
在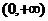 内恒成立;
内恒成立;
当 要使
要使 恒成立,则
恒成立,则 ,解得
,解得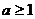 ,
,
当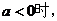
 恒成立,
恒成立,
所以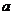 的取值范围为
的取值范围为 .
.
根据题意得: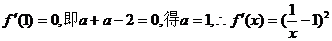 ,
,
于是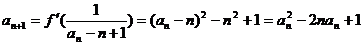 ,
,
用数学归纳法证明如下:
当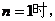
 ,不等式成立;
,不等式成立;
假设当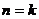 时,不等式
时,不等式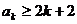 成立,即
成立,即 也成立,
也成立,
当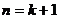 时,
时, ,
,
所以当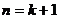 ,不等式也成立,
,不等式也成立,
综上得对所有 时,都有
时,都有 .
.
(3) 由(2)得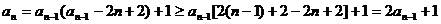 ,
,
于是
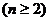 ,
,
所以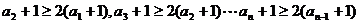 ,
,
累乘得: ,
,
所以 .
.
64、(湖北省武汉市武昌区2008届高中毕业生元月调研测试)已知函数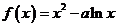 在区间(1,2 ]上是增函数,
在区间(1,2 ]上是增函数, 在区间(0,1)上为减函数.
在区间(0,1)上为减函数.
(Ⅰ)试求函数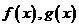 的解析式;
的解析式;
(Ⅱ)当 x >0时,讨论方程 解的个数.
解的个数.
解: (Ⅰ) 在
在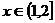 恒成立,
恒成立,
所以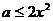 ,
,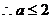 .
.
又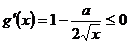 在
在 恒成立,
恒成立,
所以  ,
, .
…………………………………4分
.
…………………………………4分
从而有 .
.
故 ,
, .
…………………………6分
.
…………………………6分
(Ⅱ)令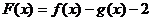 ,
,
则
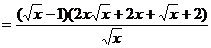
所以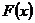 在
在 上是减函数,在
上是减函数,在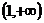 上是增函数,
……………………9分
上是增函数,
……………………9分
从而当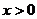 时,
时,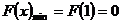 .
.
所以方程 在
在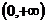 只有一个解
只有一个解 . ……………………12分
. ……………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com