
63、(湖北省随州市2008年高三五月模拟)函数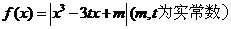 是偶函数。
是偶函数。
⑴求实数 的值;
的值;
⑵比较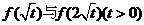 的大小;
的大小;
⑶求函数 在区间
在区间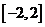 上的最大值
上的最大值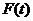 。
。


62、(湖北省荆州市2008届高中毕业班质量检测)设函数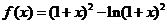
⑴求 的单调区间;
的单调区间;
⑵若关于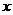 的方程
的方程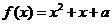 在区间
在区间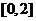 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数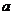 的取值范围。
的取值范围。
解:⑴定义域为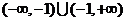 ,因为
,因为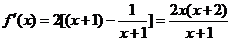
所以,当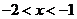 或
或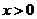 时,
时,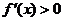
当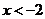 或
或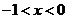 时,
时,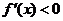
故 的单调递增区间是
的单调递增区间是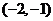 和
和
 的单调递减区间是
的单调递减区间是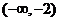 和
和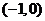 (6分)
(6分)
(注: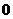 和
和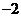 处写成“闭的”亦可)
处写成“闭的”亦可)
⑵由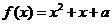 得:
得: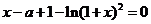 ,
,
令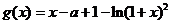 ,则
,则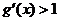 或
或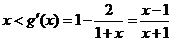
所以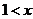 ≤
≤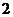 时,
时,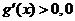 ≤
≤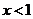 时,
时,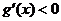
故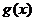 在
在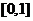 上递减,在
上递减,在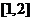 上递增
(8分)
上递增
(8分)
要使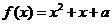 在
在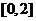 恰有两相异实根,则必须且只需
恰有两相异实根,则必须且只需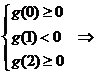
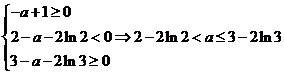
即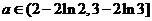
61、(湖北省荆门市2008届上期末)设函数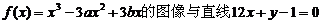 相切于点(1,-11)。
相切于点(1,-11)。
(1)求a,b的值;
(2)讨论函数 的单调性。
的单调性。
解:(1)求导得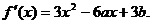 ………………2分
………………2分
由于 相切与点(1,-11),
相切与点(1,-11),
所以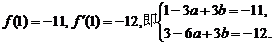 ………………5分
………………5分
解得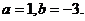 ………………6分
………………6分
(2)由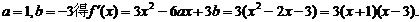
令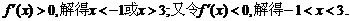
所以当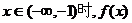 是增函数, ………………8分
是增函数, ………………8分
当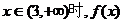 也是增函数; ………………10分
也是增函数; ………………10分
当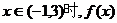 是减函数。
是减函数。
60、(湖北省荆门市2008届上期末)已知函数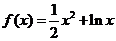 .
.
(1)求函数 在
在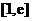 上的最大值、最小值;
上的最大值、最小值;
(2)求证:在区间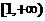 上,函数
上,函数 的图象在函数
的图象在函数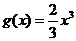 的图象的下方;
的图象的下方;
(3)求证: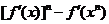 ≥
≥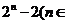 N*).
N*).
解:(1)∵f¢ (x)=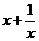 ∴当xÎ
∴当xÎ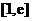 时,f¢ (x)>0, ∴
时,f¢ (x)>0, ∴ 在
在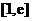 上是增函数
上是增函数
故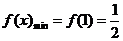 ,
,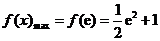 . ……………………4分
. ……………………4分
(2)设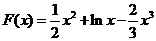 ,则
,则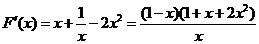 ,
,
∵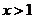 时,∴
时,∴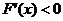 ,故
,故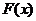 在
在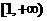 上是减函数.
上是减函数.
又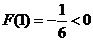 ,故在
,故在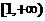 上,
上,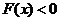 ,即
,即 ,
,
∴函数 的图象在函数
的图象在函数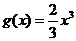 的图象的下方. ……………………8分
的图象的下方. ……………………8分
(3)∵x>0,∴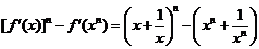 ,当
,当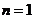 时,不等式显然成立;
时,不等式显然成立;
当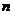 ≥
≥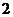 时,有
时,有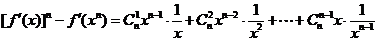
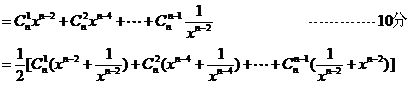
≥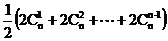
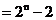
∴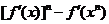 ≥
≥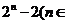 N*)
N*)
59、(湖北省黄冈市麻城博达学校2008届三月综合测试)若函数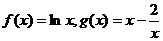
(Ⅰ)求函数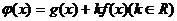 的单调区间
的单调区间
(Ⅱ)若对所有的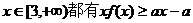 成立,求实数a的取值范围.
成立,求实数a的取值范围.
解:(1)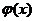 的定义域为
的定义域为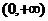 …………12分
…………12分
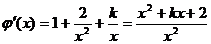 …………2分
…………2分
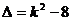
①当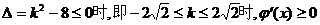 …………3分
…………3分
②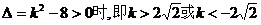 时
时
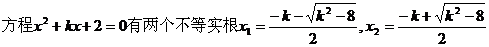
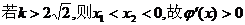 …………4分
…………4分
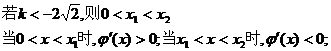
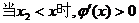 …………5分
…………5分
综上:
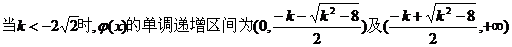
单调递减区间为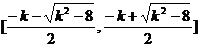
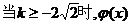 的单调递增区间(0,+
的单调递增区间(0,+ ) …………6分
) …………6分
(2)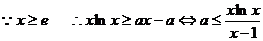 …………7分
…………7分
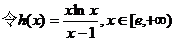 …………8分
…………8分
则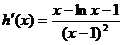 …………9分
…………9分
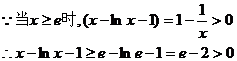
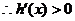 …………10分
…………10分
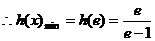 …………11分
…………11分
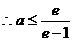 …………12分
…………12分
另解: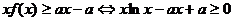
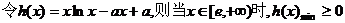 …………7分
…………7分
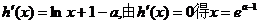 …………8分
…………8分
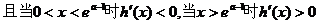
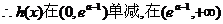 单增 …………9分
单增 …………9分
①当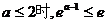
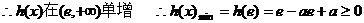
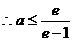 …………11分
…………11分
②当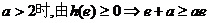
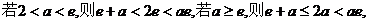
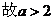 不成立 …………12分
不成立 …………12分
综上所述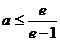
58、(湖北省三校联合体高2008届2月测试)对于函数 ,若存在
,若存在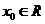 ,使
,使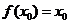 成立,则称
成立,则称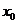 为
为 的不动点。如果函数
的不动点。如果函数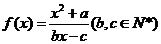 有且仅有两个不动点
有且仅有两个不动点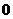 、
、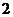 ,且
,且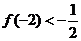 。
。
(1)试求函数 的单调区间;
的单调区间;
(2)已知各项不为零的数列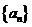 满足
满足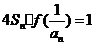 ,求证:
,求证: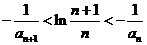 ;
;
(3)设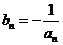 ,
,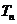 为数列
为数列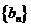 的前
的前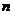 项和,求证:
项和,求证: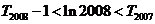 。
。
(1)设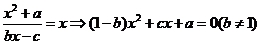
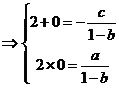 ∴
∴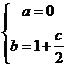 ∴
∴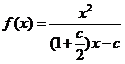
由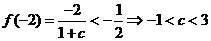
又∵ ∴
∴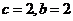
∴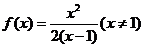 …… 3分
…… 3分
于是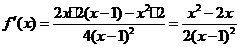
由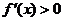 得
得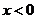 或
或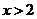 ; 由
; 由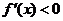 得
得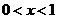 或
或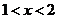
故函数 的单调递增区间为
的单调递增区间为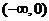 和
和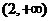 ,
,
单调减区间为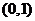 和
和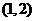 ……4分
……4分
(2)由已知可得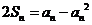 , 当
, 当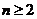 时,
时,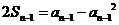
两式相减得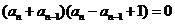
∴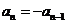 或
或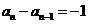
当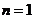 时,
时,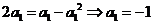 ,若
,若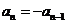 ,则
,则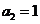 这与
这与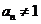 矛盾
矛盾
∴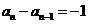 ∴
∴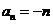 ……6分
……6分
于是,待证不等式即为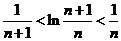 。
。
为此,我们考虑证明不等式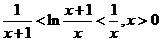
令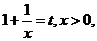 则
则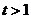 ,
,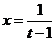
再令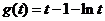 ,
,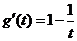 由
由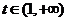 知
知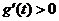
∴当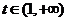 时,
时,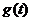 单调递增 ∴
单调递增 ∴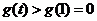 于是
于是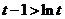
即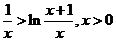 ①
①
令 ,
,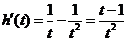 由
由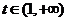 知
知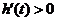
∴当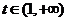 时,
时,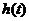 单调递增 ∴
单调递增 ∴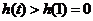 于是
于是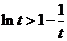
即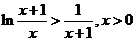 ②
②
由①、②可知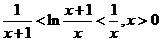 ……10分
……10分
所以,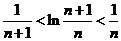 ,即
,即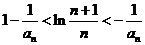 ……11分
……11分
(3)由(2)可知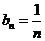 则
则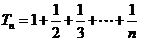
在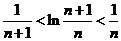 中令
中令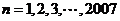 ,并将各式相加得
,并将各式相加得
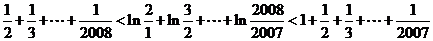
即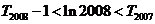 ……14分
……14分
57、(湖北省八校高2008第二次联考)已知 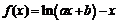 ,其中
,其中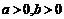 .
.
(Ⅰ)求使 在
在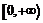 上是减函数的充要条件;
上是减函数的充要条件;
(Ⅱ)求 在
在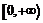 上的最大值;
上的最大值;
(Ⅲ)解不等式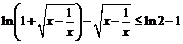 .
.
解:(1)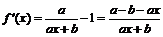 .
. 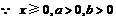 ,
, 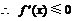 时,
时,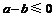 ,即
,即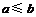 .
.
当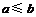 时,
时,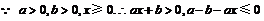 , 即
, 即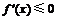 .
.
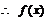 在
在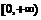 上是减函数的充要条件为
上是减函数的充要条件为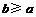 .
………(4分)
.
………(4分)
(2)由(1)知,当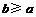 时
时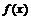 为减函数,
为减函数,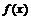 的最大值为
的最大值为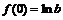 ;
;
当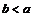 时,
时,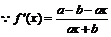 ,
, 当
当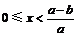 时,
时,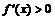 ,当
,当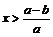 时
时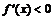 ,
,
即在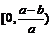 上
上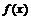 是增函数,在
是增函数,在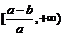 上
上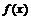 是减函数,
是减函数,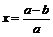 时
时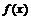 取最大值,
取最大值,
最大值为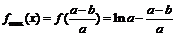 , 即
, 即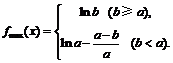 ……(13分)
……(13分)
(3)在(1)中取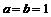 ,即
,即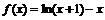 , 由(1)知
, 由(1)知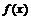 在
在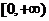 上是减函数.
上是减函数.
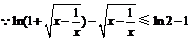 ,即
,即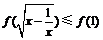 ,
,
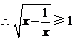 ,解得
,解得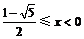 或
或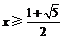 .
.
故所求不等式的解集为[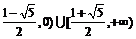 ……………(8分)
……………(8分)
56、(黑龙江省哈师大附中2008届高三上期末)已知a为实数,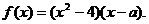
(1)若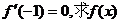 在[-4,4]上的最大值和最小值;
在[-4,4]上的最大值和最小值;
(2)若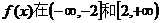 上都是递增的,求a的取值范围。
上都是递增的,求a的取值范围。
解:(1)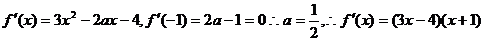
|
x |
(-∞,-1) |
-1 |
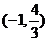 |
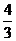 |
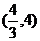 |
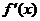 |
+ |
0 |
- |
0 |
+ |
 |
增 |
极大 |
减 |
极小 |
增 |
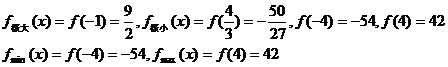
(2)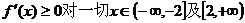 均成立,
均成立,
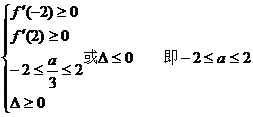
55、(黑龙江省哈尔滨三中2008年高三上期末)设函数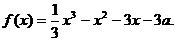
(1)如果a=1,求曲线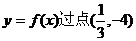 的切线方程;
的切线方程;
(2)当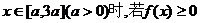 恒成立,求a的取值范围。
恒成立,求a的取值范围。
答案:(1)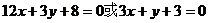
(2)a≥6
54、(黑龙江省哈尔滨三中2008年高三上期末)已知函数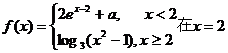 处连续。
处连续。
(1)求实数a的值;
(2)解关于x的不等式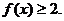
答案:(1)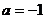
(2)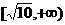
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com