
6.设{an}是首项为1的正项数列,且(n+1)an+12-nan2+an+1an=0(n∈N*),则它的通项公式an=______________.
简答.提示:1-4.CABC; 3. a1·a2·a3=(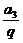 )3,故a1·a2·a3·…·a30=(
)3,故a1·a2·a3·…·a30=(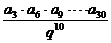 )3.又q=2,故a3·a6·a9·…·a30=220.选B;
4.特例法,设为常数列a,可知选C;
5.由题意
)3.又q=2,故a3·a6·a9·…·a30=220.选B;
4.特例法,设为常数列a,可知选C;
5.由题意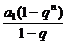 <
<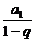 且|q|<1对n∈N都成立,∴a1>0,0<q<1.答案:(1,
且|q|<1对n∈N都成立,∴a1>0,0<q<1.答案:(1,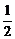 )(a1>0,0<q<1的一组数); 6. 分解因式得[(n+1)an+1-nan]·[an+1+an]=0,又an>0,则(n+1)an+1-nan=0,即
)(a1>0,0<q<1的一组数); 6. 分解因式得[(n+1)an+1-nan]·[an+1+an]=0,又an>0,则(n+1)an+1-nan=0,即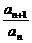 =
=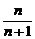 .又a1=1,由累积法可得an=
.又a1=1,由累积法可得an=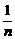 .
.
[解答题]
5.(2003上海)若首项为a1,公比为q的等比数列{an}的前n项和总小于这个数列的各项和,则首项a1,公比q的一组取值可以是(a1,q)=___________.
4. 若等比数列的各项均为正数,前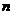 项之和为
项之和为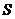 ,前
,前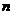 项之积为
项之积为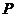 ,前
,前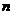 项倒数之和为
项倒数之和为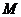 ,则 ( )
,则 ( )
(A)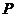 =
=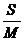 (B)
(B)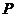 >
>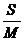 (C)
(C)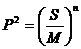 (D)
(D)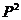 >
>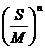
[填空题]
3.设{an}是由正数组成的等比数列,公比q=2,且a1·a2·a3·…·a30=230,那么a3·a6·a9·…·a30等于 ( )
A.210 B.220 C.216 D.215
2.在等比数列{an}中,a9+a10=a(a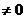 ),a19+a20=b,则a99+a100的值为
( )
),a19+a20=b,则a99+a100的值为
( )
(A)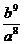 (B)(
(B)(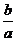 )9 (C)
)9 (C)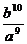 (D)(
(D)(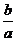 )10
)10
1.在公比q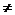 1的等比数列{an}中,若am=p,则am+n的值为
(
)
1的等比数列{an}中,若am=p,则am+n的值为
(
)
(A)pqn+1 (B)pqn-1 (C)pqn (D)pqm+n-1
3.思想.方法 :转化为基本量,利用性质,方程的思想,类比思想.
同步练习 3.4等比数列
[选择题]
2.等比数列的通项公式与前n项和公式的求法与应用;
五个元素a1,an,n,q,Sn中知三,可求另两个.次数较高时可除或换元;
1.等比数列的概念和性质,证明数列{an}是等比数列的方法:
[例1] (2006陕西) 已知正项数列{an},其前n项和Sn满足10Sn=an2+5an+6且a1,a3,a15成等比数列,求数列{an}的通项an 
解: ∵10Sn=an2+5an+6, ① 代n=1得10a1=a12+5a1+6,a1=2或a1=3
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2)
当a1=3时,a3=13,a15=73 a1, a3,a15不成等比数列∴a1≠3;
a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3=12, a15=72, 有 a32=a1a15 , ∴a1=2, ∴an=5n-3
[例2]等比数列{an}的各项均为正数,其前n项中,数值最大的一项是54,若该数列的前n项之和为Sn,且Sn=80,S2n=6560,求:
(1)前100项之和S100.
(2)通项公式an.
解:设公比为q,由已知得
Sn=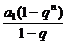 =80, ①
=80, ①
S2n=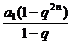 =6560, ②
=6560, ②
由②÷①解得,qn=81,q>1, (∵an>0),可知最大项为an=a1qn-1 ③
qn=81代入①③得a1=2,q=3,
(1)前100项之和S100=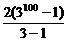 =3100-1.
=3100-1.
(2)通项公式为an=2·3n-1.
提炼方法:1.转化为基本量;2. 解方程次数较高时除一下可降次.3.判定最大项的方法.
[例3] (2005全国Ⅲ)在等差数列{an}中,公差d≠0,且a2是a1和a4的等比中项,已知a1,a3,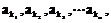 成等比数列,求数列k1,k2,k3,…,kn的通项kn
成等比数列,求数列k1,k2,k3,…,kn的通项kn
解:由题意得: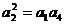
即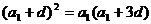
又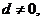
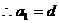 an=na1
an=na1
又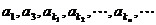 成等比数列,
成等比数列,
∴该数列的公比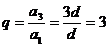 ,
,
其中第n+2项: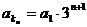
又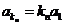
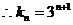 所以数列
所以数列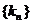 的通项为
的通项为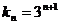
方法步骤:1.推a1=d, an=na1;q=a3÷a1=3,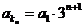 ;
;
2.比较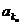 在两数列中的式子.
在两数列中的式子.
[例4]已知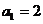 ,点
,点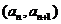 在函数
在函数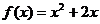 的图象上(
的图象上(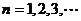 )
)
(1)证明数列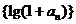 是等比数列;
是等比数列;
(2)设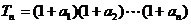 ,求
,求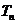 及数列
及数列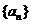 的通项;
的通项;
解:(Ⅰ)由已知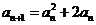 ,
,
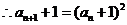
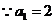
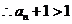 ,两边取对数得
,两边取对数得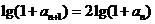 ,
,
即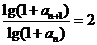
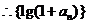 是公比为2的等比数列.
是公比为2的等比数列.
(Ⅱ)由(Ⅰ)知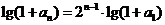
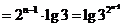
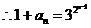 (*)
(*)
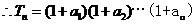
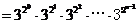
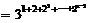 =
=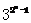
由(*)式得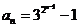
[研讨.欣赏]设数列{an},a1=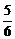 ,若以a1,a2,…,an为系数的二次方程:an-1x2-anx+1=0(n∈N*且n≥2)都有根α、β满足3α-αβ+3β=1.
,若以a1,a2,…,an为系数的二次方程:an-1x2-anx+1=0(n∈N*且n≥2)都有根α、β满足3α-αβ+3β=1.
(1)求证:{an-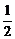 }为等比数列; (2)求an;
}为等比数列; (2)求an;
(3)求{an}的前n项和Sn.
证明(1)∵α+β=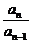 ,αβ=
,αβ=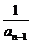 代入3α-αβ+3β=1得an=
代入3α-αβ+3β=1得an=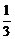 an-1+
an-1+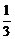 ,
,
∴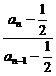 =
=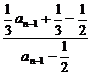 =
=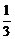 为定值.
为定值.
∴数列{an-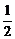 }是等比数列.
}是等比数列.
解(2)∵a1-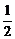 =
=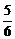 -
-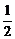 =
=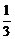 ,
,
∴an-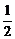 =
=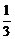 ×(
×(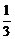 )n-1=(
)n-1=(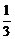 )n.
)n.
∴an=(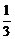 )n+
)n+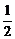 .
.
解(3)Sn=(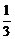 +
+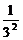 +…+
+…+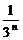 )+
)+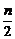 =
=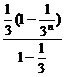 +
+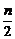 =
=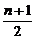 -
-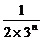 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com