
2、(江苏省启东中学2008年高三综合测试一)已知数列 的通项公式为
的通项公式为 …
… _________。
_________。
答案:2n+3n.
1、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)如图,将一个边长为1的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3)……

试用 n表示出第n个图形的边数
 .
.
答案:3×4n-1.
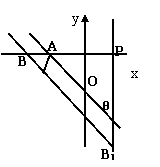
7.在平面直角坐标系中,在y轴的正半轴(原点除外)上给定两点A(0,a)、B(0,b)(a>b>0).试在x轴的正半轴(原点除外)上求点C,使∠ACB取得最大值,并求出这个最大值.
解:由题意作下图,设C(x,0),其中x>0.
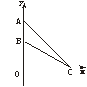
又A(0,a),B(0,b)(a>b>0),
则kAC=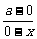 =-
=- ,
,
kBC=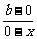 =-
=-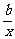 .
.
∴tan∠ACB= =
=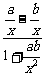 =
= ≤
≤ .此时x=
.此时x=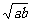 时取等号.故所求点C(
时取等号.故所求点C(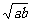 ,0),最大值为arctan
,0),最大值为arctan .
.
1. 已知△ABC的两条高线所在直线的方程为2x-3y+1=0和x+y=0,顶点A(1,2),求:
(1)BC边所在直线的方程;
(2)△ABC的面积.
解:(1)A点不在两条高线上,从而AB、AC边所在直线方程为3x+2y-7=0,x-y+1=0.
∴C(-2,-1)、B(7,-7).
∴边BC所在直线方程是2x+3y+7=0.
(2)∵|BC|= ,点A到边BC的高为h=
,点A到边BC的高为h=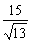 ,从而△ABC的面积是
,从而△ABC的面积是 ×3
×3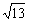 ×
×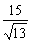 =
=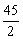 .
.
10. 已知过点A(1,1)且斜率为-m(m>0)的直线l与x轴、y轴分别交于P、Q,过P、Q作直线2x+y=0的垂线,垂足为R、S,求四边形PRSQ面积的最小值.
解:设l的方程为y-1=-m(x-1),
则P(1+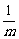 ,0),Q(0,1+m).
,0),Q(0,1+m).
从而可得直线PR和QS的方程分别为
x-2y-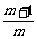 =0和x-2y+2(m+1)=0.
=0和x-2y+2(m+1)=0.
又PR∥QS,
∴|RS|=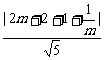
=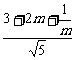 .又|PR|=
.又|PR|=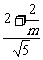 ,
,
|QS|=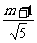 ,
,
四边形PRSQ为梯形,
S四边形PRSQ= [
[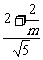 +
+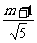 ]·
]·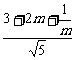
= (m+
(m+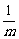 +
+ )2-
)2-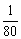 ≥
≥ (2+
(2+ )2-
)2-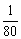 =3.6.
=3.6.
∴四边形PRSQ的面积的最小值为3.6.
[探索题] (2005上海) 已知函数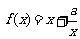 的定义域为
的定义域为 ,且
,且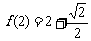 . 设点
. 设点 是函数图象上的任意一点,过点
是函数图象上的任意一点,过点 分别作直线
分别作直线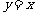 和
和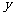 轴的垂线,垂足分别为
轴的垂线,垂足分别为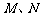 .
.
(1)求 的值;
的值;
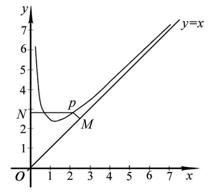 (2)问:
(2)问: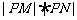 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设 为坐标原点,求四边形
为坐标原点,求四边形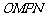 面积的最小值.
面积的最小值.
[解](1)∵ 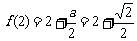 ,
,
∴ 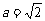 .
.
(2)设点 的坐标为
的坐标为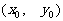 ,则有
,则有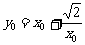 ,
, ,
,
由点到直线的距离公式可知: ,
,
故有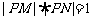 ,即
,即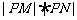 为定值,这个值为1.
为定值,这个值为1.
(3)由题意可设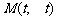 ,可知
,可知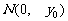 .
.
∵ 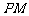 与直线
与直线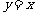 垂直,∴
垂直,∴  ,即
,即  ,解得
,解得
 ,又
,又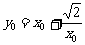 ,∴
,∴  .
.
∴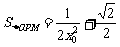 ,
, ,
,
∴  ,
,
当且仅当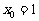 时,等号成立.
时,等号成立.
∴ 此时四边形 面积有最小值
面积有最小值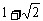 .
.
备选题
9. 已知直线 经过点P(3,1),且被两平行直线
经过点P(3,1),且被两平行直线 :x+y+1=0和
:x+y+1=0和
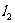 :x+y+6=0截得的线段之长为5。求直线
:x+y+6=0截得的线段之长为5。求直线 的方程。
的方程。
解法一:若直线 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为


|
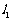 、
、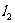 的交点分别是A1(3,-4)和
的交点分别是A1(3,-4)和
B1(3,-9),截得的线段AB的长|AB|=|-4+9|=5,
符合题意。
若直线 的斜率存在,则设
的斜率存在,则设 的方程为y=k(x-3)+1,
的方程为y=k(x-3)+1,
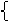 解方程组
y=k(x-3)+1
解方程组
y=k(x-3)+1
x+y+1=0
得A(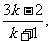 -
- )
)
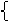 解方程组
y=k(x-3)+1
解方程组
y=k(x-3)+1
x+y+6=0
得B(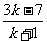 ,-
,-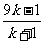 )
)
由|AB|=5得
(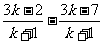 )2+(
)2+(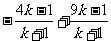 )2=25,
)2=25,
解之,得k=0,即所求的直线方程为y=1。
综上可知,所求 的方程为x=3或y=1。
的方程为x=3或y=1。
解法二:由题意,直线l1、l2之间的距离为d=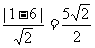 ,且直线
,且直线 被直线l1,、l2所截的线段AB的长为5,设直线l与l1的夹角为θ,则
被直线l1,、l2所截的线段AB的长为5,设直线l与l1的夹角为θ,则
sinθ=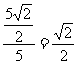 ,故θ=450。
,故θ=450。
由直线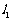 :x+y+1=0的倾斜角为1350,知直线
:x+y+1=0的倾斜角为1350,知直线 的倾斜角为00或900,又由直线
的倾斜角为00或900,又由直线 过点P(3,1),故所求
过点P(3,1),故所求 的方程为x=3或y=1。
的方程为x=3或y=1。
解法三:设直线 与
与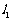 、
、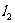 分别相交于A(x1,y1)、B(x2,y2),则x1+y1+1=0,
分别相交于A(x1,y1)、B(x2,y2),则x1+y1+1=0,
x2+y2+6=0。两式相减,得(x1-x2)+(y1-y2)=5 ①
又 (x1-x2)2+(y1-y2)2=25 ②

 联立 ① ②,可得 x1-x2=5 x1-x2=0
联立 ① ②,可得 x1-x2=5 x1-x2=0
y1-y2=0 y1-y2=5
由上可知,直线 的倾斜角为00或900,又由直线
的倾斜角为00或900,又由直线 过点P(3,1),故所求
过点P(3,1),故所求 的方程为x=3或y=1。
的方程为x=3或y=1。
8. 求满足下列条件的直线 的方程
的方程
⑴在y轴上的截距为 ,且它与两坐标轴围成的三角形面积为6
,且它与两坐标轴围成的三角形面积为6
⑵与直线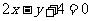 的夹角为
的夹角为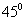 ,且交点在x轴上
,且交点在x轴上
解:⑴设直线的方程为 ,由题意得
,由题意得 ,
,
当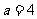 时,直线
时,直线 的方程为
的方程为 即
即
当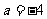 时,直线
时,直线 的方程为
的方程为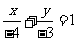 即
即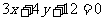
⑵直线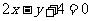 交x轴于点(
交x轴于点( ),可设
),可设 的方程为
的方程为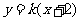
 由两直线夹角公式有
由两直线夹角公式有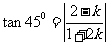 ,
,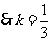
 或
或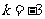


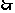
 的方程为
的方程为 或
或 ,
,
即
 或
或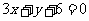

点评:求直线方程时,可根据题中已知条件适当地选择所求直线的形式,再根据题中其他条件确定方程中的待定系数
7.直线 被两条直线
被两条直线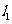 :4x+y+3=0和
:4x+y+3=0和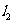 :3x─5y─5=0截得的线段中点为P(─1,2),求直线
:3x─5y─5=0截得的线段中点为P(─1,2),求直线 的方程
的方程
解:设点(a,b)在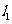 上,依题意,(─2─a,4─b)在直线
上,依题意,(─2─a,4─b)在直线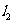 上,
上,
∴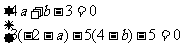 ,解之得:
,解之得:
由两点式得直线AB的方程为:3x+y+1=0
4. x=5或y=-2; 5.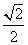 ; 6. ①
; 6. ①
[解答题]
3.解:由已知2lgsinB=lgsinA+lgsinC,
得lg(sinB)2=lg(sinA·sinC).
∴sin2B=sinA·sinC.
设l1:a1x+b1y+c1=0,l2:a2x+b2y+c2=0.
∵ =
= =
= =
= ,
,
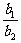 =
= ,
, 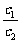 =
=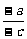 =
=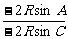 =
= ,
,
∴ =
=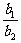 =
=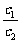 ,l1与l2重合.答案:D
,l1与l2重合.答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com