
7、(安徽省巢湖市2008届高三第二次教学质量检测)以椭圆 的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为
的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为 的两段弧,那么该椭圆的离心率等于( )
的两段弧,那么该椭圆的离心率等于( )
A.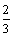 B.
B. C.
C. D.
D.
答案:B
6、(安徽省淮南市2008届高三第一次模拟考试)已知点A, F分别是椭圆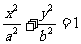 (a>b>0)的右顶点和左焦点,点B为椭圆短轴的一个端点,若
(a>b>0)的右顶点和左焦点,点B为椭圆短轴的一个端点,若 =0,则椭圆的离心率e为( ▲ )
=0,则椭圆的离心率e为( ▲ )
A.  (
( -1) B.
-1) B.  (
( -1) C.
-1) C.
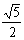 D.
D. 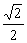
答案:A
5、(江西省五校2008届高三开学联考)从一块短轴长为2b的椭圆形玻璃镜中划出一块面积最大的矩形,其面积的取值范围是[3b2,4b2],则这一椭圆离心率e的取值范围是
A. B.
B.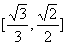 C.
C.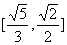 D.
D.
答案:A
4、(安徽省皖南八校2008届高三第一次联考)已知倾斜角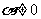 的直线
的直线 过椭圆
过椭圆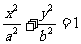
 的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则
的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则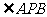 为 ( )
为 ( )
A.钝角; B.直角; C.锐角; D.都有可能;
答案:C
3、(江苏省启东中学高三综合测试四)设F1,F2是椭圆 的两个焦点,P是椭圆上的点,且
的两个焦点,P是椭圆上的点,且 ,则
,则 的面积为
( )
的面积为
( )
A.4
B.6
C.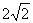 D.
D.
答案:B
2、(江苏省启东中学高三综合测试三)已知椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9,则椭圆E的离心率等于
A. B
B
 C.
C.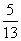 D.
D. 答案:B
答案:B
1、(江苏省启东中学高三综合测试二)在抛物线y2=2px上,横坐标为4的点到焦点的距离为5,则p的值为
A.0.5 B.1 C. 2 D. 4
答案:C
86、
85、(上海市部分重点中学2008届高三第二次联考)设 分别是椭圆C:
分别是椭圆C: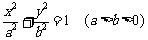 的左右焦点
的左右焦点
(1)设椭圆C上的点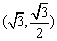 到
到 两点距离之和等于4,写出椭圆C的方程和焦点坐标
两点距离之和等于4,写出椭圆C的方程和焦点坐标
(2)设K是(1)中所得椭圆上的动点,求线段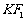 的中点B的轨迹方程
的中点B的轨迹方程
(3)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为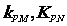 试探究
试探究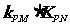 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。
[解]:(1)由于点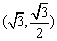 在椭圆上,
在椭圆上, ------1分
------1分
2 =4,
------2分
=4,
------2分
椭圆C的方程为  --------3分
--------3分
焦点坐标分别为(-1,0) ,(1,0)-----------4分
(2)设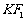 的中点为B(x, y)则点
的中点为B(x, y)则点 --------6分
--------6分
把K的坐标代入椭圆 中得
中得 -----8分
-----8分
线段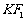 的中点B的轨迹方程为
的中点B的轨迹方程为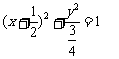 ----------10分
----------10分
(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设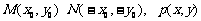 ----11分
----11分
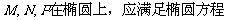 ,得
,得 ------12分
------12分
 -------------------13分
-------------------13分
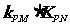 =
= =
= -----------15分
-----------15分
故: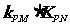 的值与点P的位置无关,同时与直线L无关,-----16分
的值与点P的位置无关,同时与直线L无关,-----16分
84、(山西大学附中2008届二月月考)已知曲线C上任意一点M到点F(0,1)的距离比它到直线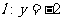 的距离小1.
的距离小1.
(1)求曲线C的方程;
(2)过点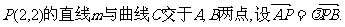 当△AOB的面积为4时(O为坐标原点),求
当△AOB的面积为4时(O为坐标原点),求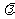 的值.
的值.
解:(1) 的距离小于1,
的距离小于1,
∴点M在直线l的上方,点M到F(1,0)的距离与它到直线 的距离相等
的距离相等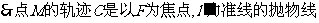 ,所以曲线C的方程为
,所以曲线C的方程为
(2)当直线m的斜率不存在时,它与曲线C只有一个交点,不合题意,
设直线m的方程为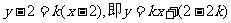 ,
,
代入 (*)
(*) 与曲线C恒有两个不同的交点 设交点A,B的坐标分别为
与曲线C恒有两个不同的交点 设交点A,B的坐标分别为 ,
,
则

点O到直线m的距离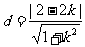 ,
,

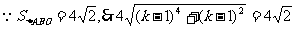 ,
,
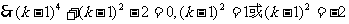 (舍去)
(舍去)

当 方程(*)的解为
方程(*)的解为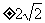 若
若
若 当
当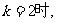 方程(☆)的解为
方程(☆)的解为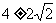
若
若 所以,
所以,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com