
43、(安徽省合肥市2008年高三年级第一次质检)设向量 ,过定点
,过定点 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点 ,以向量
,以向量 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
(1)求点P的轨迹C的方程;
(2)设过 的直线
的直线 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求 的取值范围
的取值范围
解:(1)设 ∵
∵ ,
,
∴ ,
, 2分
2分
过定点 ,以
,以 方向向量的直线方程为:
方向向量的直线方程为:
过定点 ,以
,以 方向向量的直线方程为:
方向向量的直线方程为:
联立消去 得:
得: ∴求点P的轨迹C的方程为
∴求点P的轨迹C的方程为 6分
6分
(2)当过 的直线
的直线 与
与 轴垂直时,
轴垂直时, 与曲线
与曲线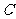 无交点,不合题意,
无交点,不合题意,
∴设直线 的方程为:
的方程为: ,
, 与曲线
与曲线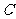 交于
交于
由


∴

 ∵
∵ ,∴
,∴ 的取值范围是
的取值范围是
42、(贵州省贵阳六中、遵义四中2008年高三联考)已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4、且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.

(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标。
解:(1)抛物线y2=2px的准线为x= - ,于是4+
,于是4+ =5,∴p=2.
=5,∴p=2.
∴抛物线方程为y2=4x……6分
(2)∵点A是坐标是(4,4), 由题意得B(0,4),M(0,2),
又∵F(1,0),∴kFA= ;MN⊥FA,∴kMN=-
;MN⊥FA,∴kMN=- ,
,
则FA的方程为y= (x-1),MN的方程为y-2= -
(x-1),MN的方程为y-2= - x,
x,

 y=
y= (x-1) x=
(x-1) x=
解方程组 ,得
y-2= - x y=
x y=
∴N的坐标( ,
, )…….12分
)…….12分
41、(广东省五校2008年高三上期末联考)椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)若 ,求m的取值范围.
,求m的取值范围.
解:(1)设C:+=1(a>b>0),设c>0,c2=a2-b2,由条件知a-c=,=,
∴a=1,b=c=,
故C的方程为:y2+=1 ………………………………………4分
(2)由=λ得-=λ(-),(1+λ)=+λ,
∴λ+1=4,λ=3 ………………………………………………6分
设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0 (*)
x1+x2=, x1x2= ………………………………………………9分
∵=3 ∴-x1=3x2 ∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k2m2+2m2-k2-2=0 ………………………………………………11分
m2=时,上式不成立;m2≠时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<- 或 <m<1
容易验证k2>2m2-2成立,所以(*)成立
即所求m的取值范围为(-1,-)∪(,1) ………………………14分
40、(广东省四校联合体第一次联考)已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为且过点(4,- )
)
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)求△F1MF2的面积.
解:(1) ∵离心率e=
∴设所求双曲线方程为x2-y2= (
( ≠0)
≠0)
则由点(4,- )在双曲线上
)在双曲线上
知 =42-(-
=42-(- )2=6
)2=6
∴双曲线方程为x2-y2=6
(2)若点M(3,m)在双曲线上
则32-m2=6 ∴m2=3
由双曲线x2-y2=6知F1(2 ,0),F2(-2
,0),F2(-2 ,0)
,0)
∴
∴ ,故点M在以F1F2为直径的双曲线上.
,故点M在以F1F2为直径的双曲线上.
(3) =
= ×2C×|M|=C|M|=2
×2C×|M|=C|M|=2 ×
× =6
=6
39、(广东省深圳市2008年高三年级第一次调研考试)在平面直角坐标系中,已知点 、
、 ,
, 是平面内一动点,直线
是平面内一动点,直线 、
、 的斜率之积为
的斜率之积为 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作直线
作直线 与轨迹
与轨迹 交于
交于 、
、 两点,线段
两点,线段 的中点为
的中点为 ,求直线
,求直线 的斜率
的斜率 的取值范围.
的取值范围.
解:(Ⅰ)依题意,有 (
( ),化简得
),化简得
 (
( ),
),
这就是动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)依题意,可设 、
、 、
、 ,则有
,则有
 ,
,
两式相减,得 ,由此得点
,由此得点 的轨迹方程为
的轨迹方程为
 (
( ).
).
设直线 :
: (其中
(其中 ),则
),则
 ,
,
故由 ,即
,即 ,解之得
,解之得 的取值范围是
的取值范围是 .
.
38、 (广东省韶关市2008届高三第一次调研考试)在平面直角坐标系
(广东省韶关市2008届高三第一次调研考试)在平面直角坐标系 中,设点
中,设点 (1,0),直线
(1,0),直线 :
: ,点
,点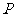 在直线
在直线 上移动,
上移动, 是线段
是线段 与
与 轴的交点,
轴的交点,  .
.
(Ⅰ)求动点 的轨迹的方程;
的轨迹的方程;
(Ⅱ) 记 的轨迹的方程为
的轨迹的方程为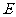 ,过点
,过点 作两条互相垂直的曲线
作两条互相垂直的曲线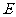 的弦
的弦 、
、 ,设
,设 、
、 的中点分别为
的中点分别为 .求证:直线
.求证:直线 必过定点
必过定点 .
.
解:(Ⅰ)依题意知,直线 的方程为:
的方程为: .点
.点 是线段
是线段 的中点,且
的中点,且 ⊥
⊥ ,∴
,∴ 是线段
是线段 的垂直平分线.…………………….2分
的垂直平分线.…………………….2分
∴ 是点
是点 到直线
到直线 的距离.
的距离.
∵点 在线段
在线段 的垂直平分线,∴
的垂直平分线,∴ .…………4分
.…………4分
故动点 的轨迹
的轨迹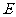 是以
是以 为焦点,
为焦点, 为准线的抛物线,其方程为:
为准线的抛物线,其方程为: . ……….7分
. ……….7分
(Ⅱ) 设 ,
, ,直线AB的方程为
,直线AB的方程为 …………….8分
…………….8分
则
(1)-(2)得 ,即
,即 ,……………………………………9分
,……………………………………9分
代入方程 ,解得
,解得 .
.
所以点M的坐标为 .……………………………………10分
.……………………………………10分
同理可得: 的坐标为
的坐标为 .
.
直线 的斜率为
的斜率为 ,方程为
,方程为
 ,整理得
,整理得 ,………………12分
,………………12分
显然,不论 为何值,
为何值, 均满足方程,
均满足方程,
所以直线 恒过定点
恒过定点
 .………………14
.………………14
37、(广东省汕头市澄海区2008年第一学期期末考试)已知椭圆 的离心率为
的离心率为 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且 ,定点A(-4,0).
,定点A(-4,0).
(1)求证:当 时.,
时., ;
;
(2)若当 时有
时有 ,求椭圆C的方程;
,求椭圆C的方程;
(3)在(2)的条件下,当M、N两点在椭圆C运动时,当 的值为6
的值为6 时, 求出直线MN的方程.
时, 求出直线MN的方程.
 解:(1)设
解:(1)设 ,
,
则 ,
,
当 时,
时, ,
,
由M,N两点在椭圆上,
若 ,则
,则 (舍去),
(舍去), (4分)
(4分)
 。(5分)
。(5分)
(2)当 时,不妨设
时,不妨设 (6分)
(6分)
又 ,
, ,
(8分)
,
(8分)
椭圆C的方程为 。 (9分)
。 (9分)
(3)因为 =6
=6 , (10分)
, (10分)
由(2)知点F(2,0), 所以|AF|=6, 即得|yM-yN|= (11分)
(11分)
当MN⊥x轴时, |yM-yN|=|MN|= ,
故直线MN的斜率存在, (12分)
,
故直线MN的斜率存在, (12分)
不妨设直线MN的方程为
联立 ,得
,得 ,
,
 =
= ,
解得k=±1。
,
解得k=±1。
此时,直线的MN方程为 ,或
,或 。 (14分)
。 (14分)
35、(广东省揭阳市2008年第一次模拟考试)设直线 与椭圆
与椭圆 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明: ;
;
(2)若 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
(1)证明:由
 得
得
将 代入
代入 消去
消去 得
得
 ①
………………………… 3分
①
………………………… 3分
由直线l与椭圆相交于两个不同的点得
 整理得
整理得 ,即
,即 ………5分
………5分
(2)解:设 由①,得
由①,得
∵ 而点
而点 , ∴
, ∴
得 代入上式,得
代入上式,得 ……………8分
……………8分
于是,△OAB的面积

 --------11分
--------11分
其中,上式取等号的条件是 即
即 ……………………12分
……………………12分
由 可得
可得
将 及
及 这两组值分别代入①,均可解出
这两组值分别代入①,均可解出
∴△OAB的面积取得最大值的椭圆方程是
 36、(广东省汕头市潮阳一中2008年高三模拟考试)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点。
36、(广东省汕头市潮阳一中2008年高三模拟考试)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点。
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.
解:(1)设椭圆方程为
则
∴椭圆方程为
(2)∵直线l平行于OM,且在y轴上的截距为m
又KOM=
 ……………………………………………………5分
……………………………………………………5分
由 ……………………………………6分
……………………………………6分
∵直线l与椭圆交于A、B两个不同点,

(3)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可…………9分
设 ……………………10分
……………………10分
则
由
 ……………………………………………………10分
……………………………………………………10分
而


故直线MA、MB与x轴始终围成一个等腰三角形.……………………14分
34、(广东省揭阳市2008年高中毕业班高考调研测试)设动点 到定点
到定点
 的距离比它到
的距离比它到 轴的距离大1,记点
轴的距离大1,记点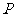 的轨迹为曲线
的轨迹为曲线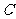 .
.
(1)求点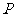 的轨迹方程;
的轨迹方程;
(2)设圆 过
过
 ,且圆心
,且圆心 在曲线
在曲线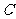 上,
上, 是圆
是圆 在
在 轴上截得的弦,试探究当
轴上截得的弦,试探究当 运动时,弦长
运动时,弦长 是否为定值?为什么?
是否为定值?为什么?
解:(1)依题意知,动点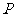 到定点
到定点
 的距离等于
的距离等于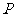 到直线
到直线 的距离,曲线
的距离,曲线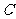 是以原点为顶点,
是以原点为顶点,
 为焦点的抛物线………………………………2分
为焦点的抛物线………………………………2分
 ∵
∵ ∴
∴
∴ 曲线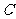 方程是
方程是 ………4分
………4分
(2)设圆的圆心为 ,∵圆
,∵圆 过
过
 ,
,
∴圆的方程为  ……………………………7分
……………………………7分
令 得:
得:
设圆与 轴的两交点分别为
轴的两交点分别为 ,
,
方法1:不妨设
 ,由求根公式得
,由求根公式得
 ,
, …………………………10分
…………………………10分
∴
又∵点 在抛物线
在抛物线 上,∴
上,∴ ,
,
∴  ,即
,即 =4--------------------------------------------------------13分
=4--------------------------------------------------------13分
∴当 运动时,弦长
运动时,弦长 为定值4…………………………………………………14分
为定值4…………………………………………………14分
(方法2:∵ ,
,
∴


又∵点 在抛物线
在抛物线 上,∴
上,∴ ,
∴
,
∴ 

∴当 运动时,弦长
运动时,弦长 为定值4)
为定值4)
33、(广东省惠州市2008届高三第三次调研考试)已知圆 :
: .
.
(1)直线 过点
过点 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
(2)过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
解(Ⅰ)①当直线 垂直于
垂直于 轴时,则此时直线方程为
轴时,则此时直线方程为 ,
,
 与圆的两个交点坐标为
与圆的两个交点坐标为 和
和 ,其距离为
,其距离为 ,满足题意……… 2分
,满足题意……… 2分
②若直线 不垂直于
不垂直于 轴,设其方程为
轴,设其方程为 ,
,
即 …………………………………………………… 3分
…………………………………………………… 3分
设圆心到此直线的距离为 ,则
,则 ,得
,得
∴ ,
, ,
,
故所求直线方程为 ……………………………………5分
……………………………………5分
综上所述,所求直线为 或
或 …………………… 6分
…………………… 6分
(Ⅱ)设点 的坐标为
的坐标为 ,
, 点坐标为
点坐标为 ,则
,则 点坐标是
点坐标是 …… 7分
…… 7分
∵ ,∴
,∴ 即
即 ,
,
 …………9分
…………9分
又∵ ,∴
,∴ …………………………… 10分
…………………………… 10分
由已知,直线m ∥ox轴,所以, ,…………………………… 11分
,…………………………… 11分
∴ 点的轨迹方程是
点的轨迹方程是 ,…………………… 12分
,…………………… 12分
轨迹是焦点坐标为 ,长轴为8的椭圆,
,长轴为8的椭圆,
并去掉 两点。
两点。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com