
16.(本小题满分14分)
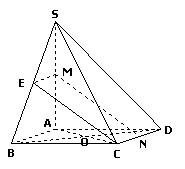 (Ⅰ)证明:如图,取
(Ⅰ)证明:如图,取 中点
中点 ,连结
,连结 、
、 ,
,
因为 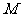 为
为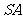 的中点,
的中点,
所以  ∥
∥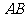 ,且
,且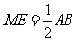 ,
,
因为  为
为 边
边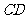 的中点,
的中点,
所以 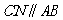 且
且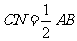 ,
,
所以 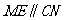 ,且
,且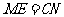 ,
,
所以 四边形 是平行四边形,
是平行四边形,
所以 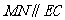 ,
,
又因为 ,
, 平面
平面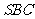 ,
,
所以直线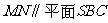 .
……………………………5分
.
……………………………5分
(Ⅱ)证明:如图,连结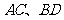 ,相交于点
,相交于点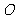 ,
,
因为 ,
,
 所以
所以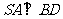 .
.
因为四边形 是菱形,
是菱形,
所以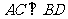 .
.
又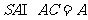 ,
,
所以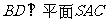 .
.
又 平面
平面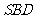 ,
,
所以平面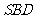
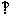 平面
平面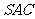 .
……………………………10分
.
……………………………10分
(Ⅲ)解:如图,连结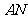 ,因为
,因为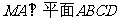 ,
,
所以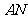 是
是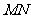 在平面
在平面 上的射影,
上的射影,
 所以
所以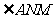 是直线
是直线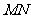 与平面
与平面 所成的角.
所成的角.
设 ,
,
由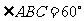 ,
,
可知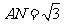 ,
,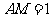 ,
,
所以在 中
中 ,
,
即直线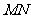 与平面
与平面 所成的角为
所成的角为 .
……………………………14分
.
……………………………14分
也可用空间向量来解决本题(略)
15.(本小题满分13分)
解:(Ⅰ)根据三角函数的定义,得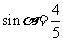 ,
, .
.
又 是锐角,所以,
是锐角,所以,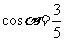 .……………………………4分
.……………………………4分
(Ⅱ)由(Ⅰ)知,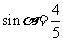 ,
, .
.
又 是锐角,
是锐角,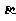 是钝角,
是钝角,
所以 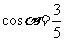 ,
,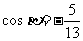 .
.
所以 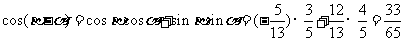 .……9分
.……9分
(Ⅲ)由题意可知,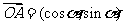 ,
,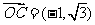 .
.
所以
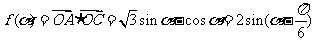 ,
,
因为  ,所以
,所以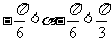 ,
,
所以函数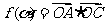 的值域为
的值域为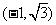 .……………………………13分
.……………………………13分
9.  ,
,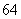 10.②和④ 11.
10.②和④ 11. 12.
12.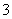 ,
,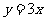 13.
13.  14.
14. 
1. C 2. B 3. D 4. B 5. D 6. A 7. C 8. A
第Ⅱ卷(共110分)
20.(本题满分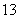 分)设
分)设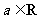 ,函数
,函数 .
.
(Ⅰ)若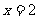 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若函数 在
在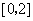 上是单调减函数,求实数
上是单调减函数,求实数 的取值范围.
的取值范围.
广州市东风中学2010-2011年度高三综合训练(6)
理科数学 一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,只有一项是符合题目要求的.选出符合题目要求的一项填在机读卡上.
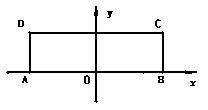
19.(本小题满分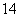 分)已知矩形
分)已知矩形 中,
中,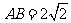 ,
, .以
.以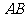 的中点
的中点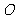 为原点建立如图所示的平面直角坐标系
为原点建立如图所示的平面直角坐标系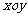 .
.
(Ⅰ)求以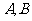 为焦点,且过
为焦点,且过 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(Ⅱ)过点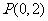 的直线
的直线 与(Ⅰ)中的椭圆交于
与(Ⅰ)中的椭圆交于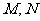 两点,是否存在直线
两点,是否存在直线 ,使得以线段
,使得以线段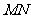 为直径的圆恰好过原点?若存在,求出直线
为直径的圆恰好过原点?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
18.(本小题满分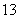 分)设数列
分)设数列 的前
的前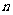 项和为
项和为 ,已知
,已知
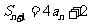 (
(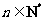 ).
).
(I)设 ,证明数列
,证明数列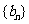 是等比数列;
是等比数列;
(II)求数列 的通项公式.
的通项公式.
17. (本小题满分
(本小题满分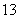 分)围建一个面积为
分)围建一个面积为 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为 的进出口,如图所示,已知旧墙的维修费用为
的进出口,如图所示,已知旧墙的维修费用为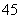 元/
元/ ,新墙的造价为
,新墙的造价为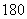 元/
元/ ,设利用的旧墙的长度为
,设利用的旧墙的长度为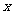 (单位:米).
(单位:米).
(Ⅰ)将修建围墙的总费用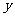 表示成
表示成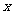 的函数;
的函数;
(Ⅱ)当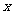 为何值时,修建此矩形场地围墙的总费用最小?
为何值时,修建此矩形场地围墙的总费用最小?
并求出最小总费用.
16.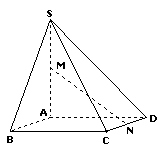 (本小题满分
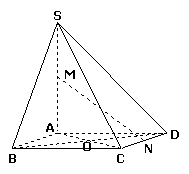
(本小题满分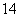 分)如图,在四棱锥
分)如图,在四棱锥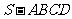 中,底面
中,底面 是棱形,
是棱形,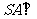 平面
平面 ,
,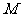 ,
, 分别为
分别为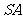 ,
,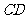 的中点.
的中点.
(Ⅰ)证明:直线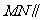 平面
平面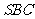 ;
;
(Ⅱ)证明:平面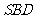
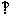 平面
平面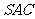 ;
;
(Ⅲ)当 ,且
,且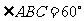 时,求直线
时,求直线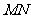 与平面
与平面 所成角的大小.
所成角的大小.
15.(本小题满分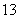 分)如图,在平面直角坐标系中,锐角
分)如图,在平面直角坐标系中,锐角 和钝角
和钝角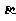 的终边分别与单位圆交于
的终边分别与单位圆交于 ,
, 两点.
两点.
(Ⅰ)如果 ,
, 两点的纵坐标分别为
两点的纵坐标分别为 ,
,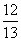 ,求
,求 和
和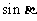 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求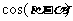 的值;
的值;
 (Ⅲ)已知点
(Ⅲ)已知点
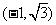 ,求函数
,求函数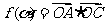 的值域.
的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com