20．（Ⅰ）解：（1）当k＝2时，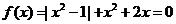　

（II）若关于的方程在上有两个解，求的取值范围，并证明．

（I）若，求方程的解；

20．已知．

又  BF平面BFM，所以BF//平面AEC.

连结BM、BD，设BDAC=O，则O为BD的中点.

所以  BM//OE.  ②

由①、②知，平面BFM//平面AEC.

由   知E是MD的中点.

  取PE的中点M，连结FM，则FM//CE.  ①

19．（Ⅰ）证明  因为底面ABCD是菱形，∠ABC=60°，

所以AB=AD=AC=a，  在△PAB中，

由PA²+AB²=2a²=PB²   知PA⊥AB.

同理，PA⊥AD，所以PA⊥平面ABCD.

（II）当F是棱PC的中点时，BF//平面AEC，证明如下，

PB=PD=,点E在PD上，且PE:ED=2:1.

（I）证明PA⊥平面ABCD；

（II）在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论.