
2、 设点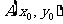 为角
为角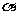 终边上任意一点,那么:(设
终边上任意一点,那么:(设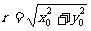 )
)
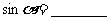 ,
,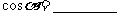 ,
,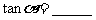 .
.
1、 设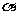 是一个任意角,它的终边与单位圆交于点
是一个任意角,它的终边与单位圆交于点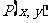 ,那么:
,那么:
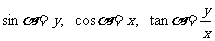 .
.
3、弧长公式:. 4、扇形面积公式: .
§1.2.1、任意角的三角函数
1、 把长度等于半径长的弧所对的圆心角叫做1弧度的角.2、 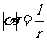 .
.
2、 与角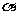 终边相同的角的集合:
.
终边相同的角的集合:
.
§1.1.2、弧度制
1、 正角、负角、零角、象限角的概念.
A组
(1)
若角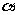 的终边过点
的终边过点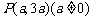 ,则
,则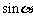 的值为( )
的值为( )
(A)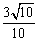 (B)
(B)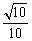 (C)
(C) 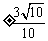 (D)
(D) 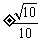
(2)
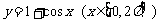 的图象与直线
的图象与直线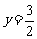 的交点的个数为( )
的交点的个数为( )
(A)0 (B)1 (C)2 (D)3
(3)在△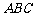 中,
中,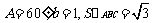 ,则
,则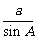 的值为( )
的值为( )
(A)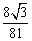 (B)
(B)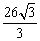 (C)
(C)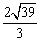 (D)
(D)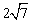
(4)化简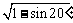 的结果是( )
的结果是( )
(A)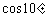 (B)
(B) (C)
(C) 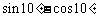 (D)
(D) 
(5)在△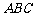 中,若
中,若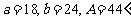 ,则此三角形解的情况为( )
,则此三角形解的情况为( )
(A)无解 (B)两解 (C)一解 (D)解的个数不能确定
(6)若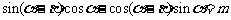 ,且
,且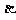 为第三象限角,则
为第三象限角,则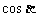 的值为( )
的值为( )
(A)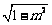 (B)
(B) 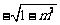 (C)
(C) 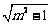 (D)
(D) 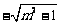
(7)有以下四种变换方式:
①
向左平行移动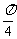 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的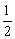 ;
;
②
向右平行移动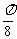 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的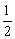 ;
;
③
每个点的横坐标缩短为原来的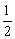 ,再向右平行移动
,再向右平行移动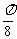 个单位长度;
个单位长度;
④
每个点的横坐标缩短为原来的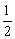 ,再向左平行移动
,再向左平行移动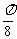 个单位长度.
个单位长度.
其中能将函数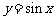 的图象变为函数
的图象变为函数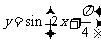 的图象的是( )
的图象的是( )
(A)①和④ (B)①和③ (C)②和④ (D)②和③
(8)在△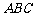 中,若
中,若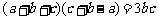 ,则
,则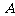 =( )
=( )
(A)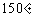 (B)
(B)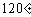 (C)
(C)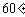 (D)
(D)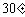
(9)已知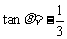 ,则
,则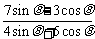 的值为
.
的值为
.
(10)函数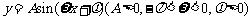 在一个周期的区间上的图象如图,
在一个周期的区间上的图象如图,
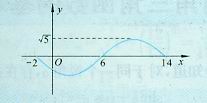 则
则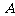 = ,
= , =
,
=
,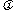 =
.
=
.
(11)已知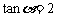 ,
,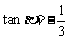 ,其中
,其中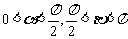 .
.
(1)求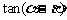 ;
;
(2)求 的值.
的值.
(12)已知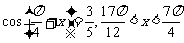 ,求
,求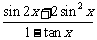 的值.
的值.
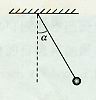 (13)一个单摆如图所示,小球偏离铅垂方向的角为
(13)一个单摆如图所示,小球偏离铅垂方向的角为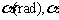 作为时间
作为时间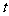 的函数,满足关系
的函数,满足关系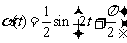 .
.
求:(1)最初时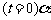 的值是多少?
的值是多少?
(2)单摆摆动的频率是多少?
(3)经过多长时间单摆完成5次完整摆动?
(14)
已知函数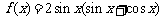 .
.
(1)求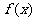 的最小正周期;
的最小正周期;
(2)画出函数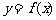 在区间
在区间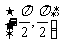 上的图象.
上的图象.
(15)
已知函数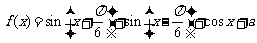 的最大值为1.
的最大值为1.
(1)求常数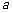 的值;(2)求使
的值;(2)求使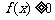 成立的x的取值集合.
成立的x的取值集合.
B组
(16)
设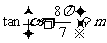 ,则
,则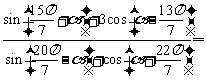
(17)
观察以下各等式: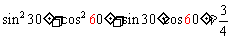 ,
,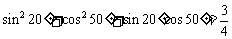 ,
,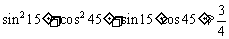 ,…,归纳得到
.
,…,归纳得到
.
(18)已知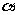 为第二象限的角,化简:
为第二象限的角,化简: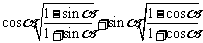
(19)已知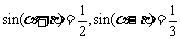 ;
;
(1)求证: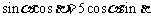 ;
;
(2)求证: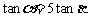 .
.
(20)
如图为一个观览车示意图.该观览车圆半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈.途中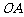 与地面垂直.以
与地面垂直.以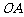 为始边,逆时针转动
为始边,逆时针转动 角到
角到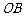 .设
.设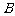 点与地面距离为
点与地面距离为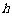 .(1)求
.(1)求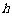 与
与 的函数解析式;(2)设从
的函数解析式;(2)设从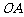 开始转动,经过
开始转动,经过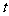 秒到达
秒到达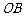 ,求
,求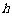 与
与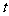 的函数解析式;(3)填写下列表格:
的函数解析式;(3)填写下列表格:

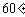
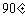
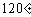
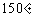
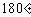
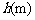
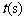 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
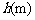 |
|
|
|
|
|
|
|
(21)
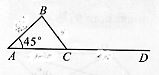
 一次机器人足球比赛中,甲队1号机器人由点
一次机器人足球比赛中,甲队1号机器人由点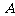 开始作匀速直线运动,到达点
开始作匀速直线运动,到达点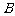 时,发现足球在点
时,发现足球在点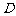 处正以2倍于自己的速度向点
处正以2倍于自己的速度向点 作匀速直线滚动.如图所示,已知
作匀速直线滚动.如图所示,已知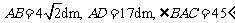 .若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?
.若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?
10.已知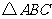 的周长为
的周长为 ,且
,且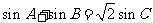 .
.
(I)求边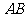 的长;1(II)若
的长;1(II)若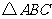 的面积为
的面积为 ,求角
,求角 的度数.60
的度数.60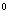
9.在△ABC中,已知角A为锐角,且
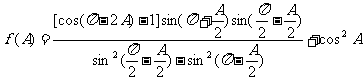 .
.
(I)求f (A)的最大值;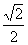 sin(2A+
sin(2A+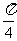 )+
)+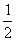
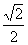 +
+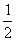
(II)若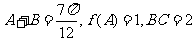 ,求△ABC的三个内角和AC边的长.
,求△ABC的三个内角和AC边的长.
8.在△ 中,角
中,角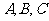 所对的边分别为
所对的边分别为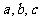 ,已知
,已知 ,
,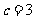 ,
,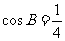 .
.
(1)求 的值;
的值;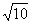 (2)求
(2)求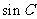 的值.
的值.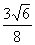
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com