
7.右图是一个纵横对折法某次试验后得到两个试验点A1、B1,
比较试验结果表明B1比A1好,则存优范围(ⅠⅡ分别表示
两个因素)是15≤Ⅰ≤30,20≤Ⅱ≤40 ;
[解析]:由纵横对折法可知,丢弃包括A1所在的班个平面区域,即去掉左半部分,所以存优范围是15≤Ⅰ≤30,20≤Ⅱ≤40 ;
6.复数 且
且 ,则
,则 的值为
的值为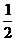 ;
;
 [解]∵
[解]∵ 所以
所以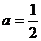 .
.
5..对于正实数 ,记
,记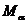 为满足下述条件的函数
为满足下述条件的函数 构成的集合:
构成的集合: 且
且 ,有
,有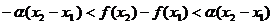 .下列结论中正确的是 ( C )
.下列结论中正确的是 ( C )
A.若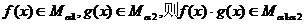 ,
,
B.若 ’
’
C.若 ,
, 
D.若 .
.
[解]对于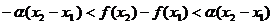 ,即有
,即有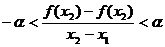

,令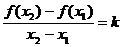 ,有
,有 ,不妨设
,不妨设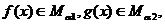 即有
即有 ,因此有
,因此有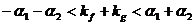 ,因此有
,因此有 ,故应选C.
,故应选C.
4.已知双曲线E的离心率为e,左、右两焦点分别为F1、F2,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a 2(其中a、c分别为双曲线的实半轴长和半焦距),则e的值为 ( A
)
A. B.
3 C.
D.

[解析]A
如右图所示,设点P的坐标为(x0,y0),由抛物线以F2为顶点,F1为焦点,可得其准线的方程为x=3c, 根据抛物线的定义可得|PF1|=|PR|=3c-x0,又由点P为双曲线上的点,根据双曲线的第二定义可得
 =e, 即得|PF2|=ex0-a,
=e, 即得|PF2|=ex0-a, 
由已知a|PF2|+c|PF1|=8a2,可得-a2+3c2=8a2,即e2=3,
由e>1可得e=, 故应选A.
3. 已知直线 交于A、B两点,O是坐标原点,向量
交于A、B两点,O是坐标原点,向量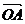 、
、 满足
满足 ,则实数a的值是(C)
,则实数a的值是(C)
A.2 B.-2 C.2或-2 D. 或-
或-

[解]由 可知
可知 ,由直线x+y=a的斜率为-1,结合图形不难知:
,由直线x+y=a的斜率为-1,结合图形不难知:
-a=-2或2,则a=2或-2,故应选C.
2. 已知函数
已知函数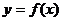
 满足
满足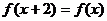 ,且
,且 时,
时, ,则
,则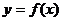 与
与 的图象的交点个数为( D )
的图象的交点个数为( D )
A.1
B.5
C.7
D.9









[解]由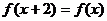 知函数
知函数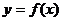 的周期为2,所以两个函数的图象如下图:
的周期为2,所以两个函数的图象如下图:
函数 恒过点(1,0),且当x=10时,lgx=1,所以两函数图象共有9个交点. 故应选D.
恒过点(1,0),且当x=10时,lgx=1,所以两函数图象共有9个交点. 故应选D.
1.
设命题p:{x| |x|>1};命题q:{x| x2 + 2x –3>0},则 是
是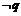 的( A )
的( A )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.即不充分也不必要条件
[解]由|x|>1得p:A={x| x>1或x<-1},又由x2 + 2x –3>0得q:B={x| x>1或x<-3};显然B是A的真子集,故q是p的充分不必要条件,从而 是
是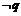 的充分不必要条件,故应选A.
的充分不必要条件,故应选A.
14.(本小题满分13分)
已知函数 ,若直线
,若直线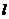 与
与  的图象都相切,且
的图象都相切,且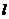 与
与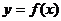 的图象相切于定点
的图象相切于定点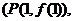
(1)求直线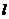 的方程及a的值;
的方程及a的值;
(2)当 时,讨论关于x的方程
时,讨论关于x的方程 的实数解的个数.
的实数解的个数.
13.(本小题满分13分)
某化工企业生产某种产品,生产每件产品的成本为3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11 – x)2万件;若该企业所生产的产品能全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数a (1≤a≤3).
(Ⅰ)求该企业正常生产一年的利润L (x)与出厂价x的函数关系式;


(Ⅱ)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润.
12.(本小题满分12分)
已知y = f (x)是定义在[–1,1]上的奇函数,x∈[0,1]时,f (x) =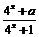 .
.
(1)求x∈[–1,0)时,y = f (x)解析式,并求y = f (x)在[0,1]上的最大值.
(2)解不等式f (x)>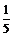 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com