
21、(本题满分12分)
已知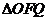 的面积为
的面积为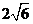 ,且
,且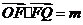 .
.
(1)当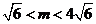 时,求向量
时,求向量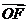 与
与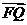 的夹角
的夹角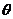 的取值范围;
的取值范围;
(2)设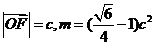 ,若以中心O为坐标原点,焦点F在非负半轴上的双曲线经过点Q,当
,若以中心O为坐标原点,焦点F在非负半轴上的双曲线经过点Q,当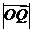 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
20、(本题满分12分)
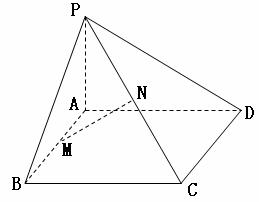
已知,如图,四边形ABCD为矩形,PA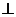 平面ABCD,M、N分别是AB、PC的中点
平面ABCD,M、N分别是AB、PC的中点
(1)求证:直线MN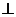 直线AB;
直线AB;
(2)若平面PDC与平面ABCD所成的二面角大小为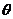 ,能否确定
,能否确定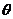 使直线MN是异面直线AB与PC的公垂线,若能确定,求出
使直线MN是异面直线AB与PC的公垂线,若能确定,求出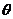 的值,若不能确定,说明理由.
的值,若不能确定,说明理由.
19、(本题满分12分)
设数列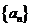 前和
前和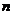 为
为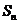 ,且
,且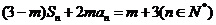 。其中
。其中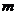 为常数,
为常数,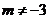 ,且
,且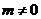 .
.
(1)求证: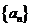 是等比数列;
是等比数列;
(2)若数列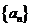 的公比
的公比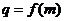 且数列
且数列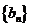 中,
中,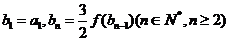 ,求证数列
,求证数列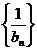 为等差数列,并求
为等差数列,并求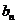 的表达式.
的表达式.
18、(本题满分12分)
从3名女运动员和2名男运动员中随机选出3位参加选拔测验,每位女运动员能通过测验的概率均为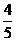 ,每位男运动员能通过测验的概率均为
,每位男运动员能通过测验的概率均为 ,试求:
,试求:
(1) 选出的3位运动员中,至少有一位男运动员的概率;
(2) 女运动员甲和男运动员乙同时被选中且通过测验的概率。
17、(本题满分12分)
已知函数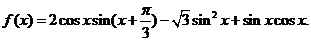
(1)
求函数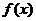 的最小正周期及单调区间;
的最小正周期及单调区间;
(2)
求函数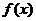 的最小值及取得最小值时相应的
的最小值及取得最小值时相应的 值。
值。
16、设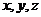 是空间的不同直线或不同平面,下列条件中能保证“若
是空间的不同直线或不同平面,下列条件中能保证“若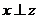 ,且
,且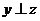 ,则
,则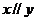 ”为真命题的是______________(填所正确条件的代号)。
”为真命题的是______________(填所正确条件的代号)。
1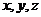 为直线 2
为直线 2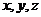 为平面
为平面
3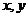 为直线,
为直线,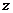 为平面 4
为平面 4 为直线,
为直线,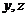 为平面
为平面
15、函数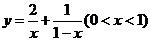 的最小值是_____________________.
的最小值是_____________________.
14、设曲线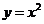 在点P处的切线斜率为3,则点P的坐标为___________________.
在点P处的切线斜率为3,则点P的坐标为___________________.
13、已知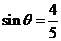 ,且
,且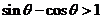 ,则
,则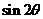 =________________.
=________________.
12、如图,是一个由三根细铁杆PA、PB、PC组成的支架,三根杆的两两夹角都是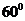 ,一个半径为1的球放在支架内,使杆与球相切,则球心到点P的距离是
,一个半径为1的球放在支架内,使杆与球相切,则球心到点P的距离是
A. 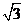
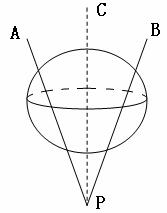 B.
B.
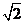
C.2
D. 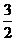
第Ⅱ卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com