
10、(苍山诚信中学·理科)已知A、B、C的坐标分别为A(3,0),B(0,3),C( ),
),

(I)若 求角
求角 的值;
的值;
(II)若 的值.
的值. 学
学
(解)(1) ,…………2分
,…………2分
 ,
,
 .……………………4分
.……………………4分
由 得
得 . 又
. 又 .…………6分
.…………6分
(2)由
 ①………………7分
①………………7分
又 ………………9分
………………9分
由①式两分平方得
 ……………………12分
……………………12分
8、(四川省绵阳市高中2009级第二次诊断性考试)在△ABC中,角A、B、C所对的边分别为a、b、c,已知向量=(c-2b,a),=(cosA,cosC),且⊥. (1)求角A的大小; (2)若=4,求边BC的最小值. 解:(1)由已知·=(c-2b,a)·(cosA,cosC)=0, 即(c-2b)cosA+acosC=0, 由争先定理,得(2RsinC-4RsinB)cosA+2rsinAcosC=0, ∴2sinBcosA=sinAcosC+sinCcosA=sin(A+C)=sinB, 由sinB≠0,得2cosA=1 Þ A=60°. (2)由已知,得=||cosA=cb·cos60°=4, ∴bc=8, 因此a2+b2+c2-bc≥2bc-bc=bc=8, 即BC的最小值为2.
7、(安徽省巢湖市2009届高三第一次教学质量检测)设 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知 ,向量
,向量  ,
, ,且
,且 与
与 共线.
共线.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)求 的值.
的值.
解:(Ⅰ)
 ,
,
 ……………………2分
……………………2分
即 ………………………………4分
………………………………4分


 ……………………………6分
……………………………6分
(Ⅱ)由

 ,
,
 ……………………………………10分
……………………………………10分
6、(福建省莆田第一中学2008-2009学年度上学期第一学段段考)设向量 ,
, ,x∈R,函数
,x∈R,函数 .
.
(Ⅰ)求函数f(x)的最小正周期和最小值;
(Ⅱ)求函数 在
在 上的单调增区间.
上的单调增区间.
解:(Ⅰ)
∵ 2分
2分
=1+ 4分
4分
∴最小正周期是 ,最小值为
,最小值为 .
6分
.
6分
(Ⅱ)解法一:因为 ,
,
令 8分
8分
得函数在 上的单调增区间为
上的单调增区间为 。
12分
。
12分
解法二:作函数 图象,由图象得函数
图象,由图象得函数 在区间
在区间 上的单调增区间为
上的单调增区间为
5、(2009届福建省福鼎一中高三理科数学强化训练综合卷一)设 、
、 是两个不共线的非零向量(
是两个不共线的非零向量( )
)
(Ⅰ)记 那么当实数t为何值时,A、B、C三点共线?
那么当实数t为何值时,A、B、C三点共线?
(Ⅱ)若 ,那么实数x为何值时
,那么实数x为何值时 的值最小?
的值最小?
解:(1)A、B、C三点共线知存在实数
即 ,…………………………………………………4分
,…………………………………………………4分
则 ………………………………………………………………6分
………………………………………………………………6分
(2)
 ……………………………9分
……………………………9分
当 ………………………………………12分
………………………………………12分
4、(江西省崇仁一中2009届高三第四次月考)已知向量 ,
, ,向量
,向量 ,
, .
.
(1)当k为何值时,向量 ;
;
(2)若向量 的夹角为钝角,求实数k的取值范围.
的夹角为钝角,求实数k的取值范围.
解: ,
, ………………1分
………………1分
(1) ,则
,则 =0,即
=0,即 ,
, ,
, ……6分
……6分
(2) 又
又 ,
, ,即
,即 …… 10分
…… 10分
但此时 ,
,
若 ,则有
,则有 ,
,
故所求实数k的取值范围是 且
且 ………………12分
………………12分
3、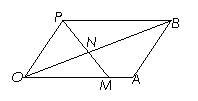 (江西省崇仁一中2009届高三第四次月考)如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若=x,=y.
(江西省崇仁一中2009届高三第四次月考)如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若=x,=y.
(1)把y用x表示出来(即求y=f(x)的解析式);
(2)设数列{an}的首项a1=1,前n项和Sn满足:
Sn=f(Sn-1)(n≥2),求数列{an}通项公式.
解:(1)==-,则=-=x-y,
=-=(-)-x=-(1+x)+
又∥,有x-y(1+x)=0,即y= (x>0);…………6分
(2)当n≥2时,由Sn=f(Sn-1)=,则==+1………8分
又S1=a1=1,那么数列{}是首项和公差都为1的等差数列,
则=1+(n-1)=n,即Sn=,……………………10分
故an==.………………12分
2、(河北省衡水中学2008-2009学年度第一学期期中考试)已知  分别是
分别是 轴、
轴、 轴方向上的单位向量,
轴方向上的单位向量, ,且
,且 ,在射线
,在射线 上从下到上依次有点
上从下到上依次有点 ,
, 且
且
(1)求 ; (2)求
; (2)求 ;
;
(3)求四边形 面积的最大值.
面积的最大值.
解:(1)


所以 -----2分
-----2分
(2)由(1)

= -------------5分
-------------5分
 且
且 均在射线
均在射线 上,
上,
 ---------------------8分
---------------------8分
(3)四边形 的面积为
的面积为
 的底边
的底边 上的高
上的高
又 ,
, 到直线
到直线 的距离为:
的距离为:


而
 -----------------------12分
-----------------------12分
1、(甘肃省兰州一中2008-2009高三上学期第三次月考)在△ABC中,
(I)求 的值;
的值;
(II)当△ABC的面积最大时,求∠A的大小。
解:(I)由已知得
因此, …………4分
…………4分
(II) , …………6分
, …………6分

 ……9分
……9分
当 …………12分
…………12分
13、已知四面体各棱长是1或2,且该四面体不是正四面体,求这个四面体体积的所有可能的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com