
5.若函数log2(kx2+4kx+3)的定义域为R,则k的取值范围是 ( )
A.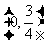 B.
B.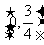 C.
C.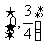 D.
D.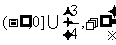
 6.下列函数图象正确的是 ( )
6.下列函数图象正确的是 ( )
A B C D
4.若a>0,b>0,ab>1,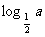 =ln2,则logab与
=ln2,则logab与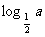 的关系是 ( )
的关系是 ( )
A.logab<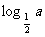 B.logab=
B.logab=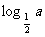
C.
logab>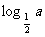 D.logab≤
D.logab≤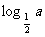
3.设函数y=lg(x2-5x)的定义域为M,函数y=lg(x-5)+lgx的定义域为N,则 ( )
A.M∪N=R B.M=N C.M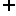 N D.M
N D.M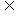 N
N
2.如果lgx=lga+3lgb-5lgc,那么 ( )
A.x=a+3b-c B.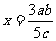 C.
C.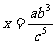 D.x=a+b3-c3
D.x=a+b3-c3
1.对数式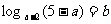 中,实数a的取值范围是 ( )
中,实数a的取值范围是 ( )
A. B.(2,5) C.
B.(2,5) C.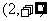 D.
D. 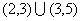
22. 解: (1)由题意得: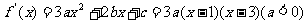
∴在(-∞,1)上,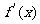 <0;
<0;
在(1,3)上,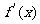 >0; 在3,+∞)上,
>0; 在3,+∞)上,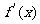 <0;
<0;
因此,f(x)在x0=1处取得极小值-4
∴a+b+c=-4 ①…

①②③联立得:
∴f(x)=-x3+6x2-9x
(2)由(1)知f(x)在x=3处取得极大值为:f(3)=0
(3)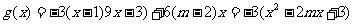
①当2≤m≤3时,
②当m<2时,g(x)在[2,3]上单调递减,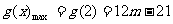
③当m>3时,g(x)在[2,3]上单调递增,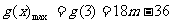
21. 解:(1)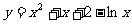 ,知x =1时,y
= 4,
,知x =1时,y
= 4,
又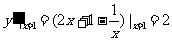
∴直线l的方程为y-4 = 2 (x-1),即y = 2x +2
又点(n-1,an+1-an-a1)在l上,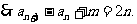
即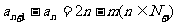

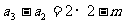
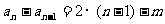
各项迭加,得
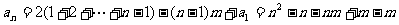
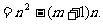
∴通式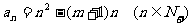
(2)∵m为奇数,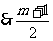 为整数,
为整数,
由题意,知a5是数列{an}中的最小项,
∴得m = 9
令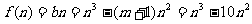
则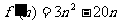 ,由
,由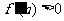 ,得
,得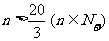
即为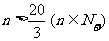 时,
时,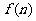 单调递增,即
单调递增,即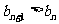 成立,
成立,
∴n的取值范围是n≥7,且
20. (1)由
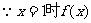 有极值,
有极值,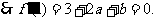 ①
①
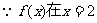 处的切线l的倾斜角为
处的切线l的倾斜角为 ②
②
由①②可解得a =-4,b = 5
设切线l的方程为y = x + m,由坐标原点(0,0)到切线l的距离为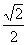 ,可得m =±1,
,可得m =±1,
又切线不过第四象限,所以m =1,切线方程为y = x + 1.
∴切点坐标为(2,3),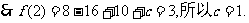
故a=-4,b = 5,c =1.
(2)由(Ⅰ)知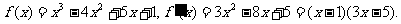
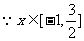 ,∴函数
,∴函数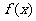 在区间[-1,1]上递增,在
在区间[-1,1]上递增,在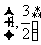 上递减,
上递减,
又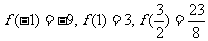 ,
,
∴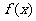 在区间
在区间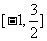 上的最大值为3,最小值为-9.
上的最大值为3,最小值为-9.
19. (1)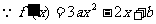 ,
,
又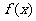 在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数,
在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数,
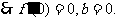
又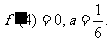
(2)
当x=1时,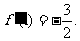
此时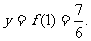
即切线的斜率为-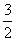 ,切点坐标为(1,
,切点坐标为(1,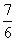 ), 所求切线方程为9x+6y-16=0.
), 所求切线方程为9x+6y-16=0.
至少有一件是次品的概率为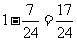
(2)设抽取n件产品作检验,则3件次品全部检验出的概率为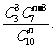
由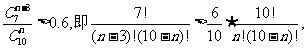 整理得:
整理得: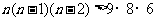 ,
,
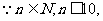 ∴当n=9或n=10时上式成立.
∴当n=9或n=10时上式成立.
答:任意取出3件产品作检验,其中至少有1件是次品的概率为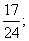 为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.
为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.
18. (1)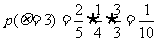
(2)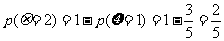
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com