
1.函数y=f(x)的图象在点P(1,f(1))处的切线方程为y=-2x+10,导函数为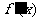 ,则f(1)+
,则f(1)+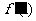 的值为
的值为
A. -2 B.2 C .6 D. 8
7.某运输公司有7辆可载的6t的A型卡车与4辆可载的10t的B型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运360t沥青的任务,已知每辆卡车每天往返的次数为A型车8次,B型车6次,每辆卡车每天往返的成本费为A型车160元,B型车为252元,每天派出A型车和B型车各多少辆,公司所花的成本费最低?
备课组长签字: 年 月 日
6.某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台。已知生产这些家电产品每台所需工时和每台产值如下表:
|
家电名称 |
空调器 |
彩电 |
冰箱 |
|
工时 |
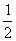 |
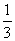 |
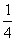 |
|
产值/千元 |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
5.某工厂生产甲、乙两种产品,计划每天生产量不少于15t,已知生产甲产品1t需煤9t,电力4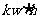 ,劳力3个;生产乙产品1t需煤4t,电力5
,劳力3个;生产乙产品1t需煤4t,电力5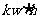 ,劳力10个;甲产品每1t利润7万元,乙产品每1t利润12万元;但每天用煤不超过300t,电力不超过200
,劳力10个;甲产品每1t利润7万元,乙产品每1t利润12万元;但每天用煤不超过300t,电力不超过200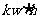 ,劳力只有300个。问每天各生产甲、乙两种产品多少,能使利润总额达到最大?
,劳力只有300个。问每天各生产甲、乙两种产品多少,能使利润总额达到最大?
4.某服装制造商现有10m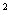 的棉布料,10m
的棉布料,10m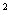 的羊毛料,和6 m
的羊毛料,和6 m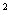 的丝绸料。做一条裤子需要1 m
的丝绸料。做一条裤子需要1 m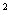 的棉布料,2 m
的棉布料,2 m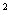 的羊毛料,1m
的羊毛料,1m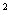 的丝绸料。一条裙子需要1 m
的丝绸料。一条裙子需要1 m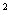 的棉布料,1 m
的棉布料,1 m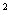 的羊毛料,1m
的羊毛料,1m 的丝绸料。一条裤子的收益是20元,一条裙子的收益是40元。为了使收益达到最大,需要同时生产这两种服装,请你列出生产这两种服装件数所满足的数学关系式,并画出图形。
的丝绸料。一条裤子的收益是20元,一条裙子的收益是40元。为了使收益达到最大,需要同时生产这两种服装,请你列出生产这两种服装件数所满足的数学关系式,并画出图形。
3.已知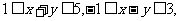 求
求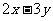 的取值范围。
的取值范围。
2.给定下面的线性规划问题:求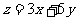 的最大值与最小值,使
的最大值与最小值,使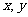 满足约束条件
满足约束条件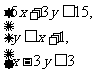 要使目标函数只有最小值而无最大值,请你改造条件中的一个不等式,那么新的约束条件应该是______________________。
要使目标函数只有最小值而无最大值,请你改造条件中的一个不等式,那么新的约束条件应该是______________________。
1.不等式组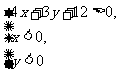 表示的平面区域内的整点坐标是_____________________________
表示的平面区域内的整点坐标是_____________________________
2. 电视台应某企业之约播放两套连续剧。其中,连续剧甲每次播放时间为80min,其中广告时间为1min,收视观众为60万;连续剧乙每次播放时间为40min,其中广告时间为1min,收视观众为20万。已知此企业与电视台达成协议,要求电视台每周至少播放6min广告,而电视台每周只能为该企业提供不多于320min的节目时间。如果你是电视台的制片人,电视台每周应播映两套连续剧各多少次,才能获得最高的收视率?
课外活动:
1. 给出平面区域如图1,若使目标函数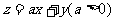 取得最大值的最优解有无穷多个,则
取得最大值的最优解有无穷多个,则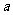 的值为___________。
的值为___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com