
8.求证:(1)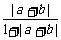 ≤
≤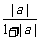 +
+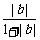 .
.
(2) 如果设m等于 ,
,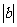 和1中最大的一个,
和1中最大的一个,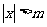 时,则
时,则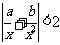 .
.
证明(1):令f(x)=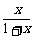 (x≥0),易证f(x)在[0,+∞)上单调递增.
(x≥0),易证f(x)在[0,+∞)上单调递增.
|a+b|≤|a|+|b|,
∴f(|a+b|)≤f(|a|+|b|),
即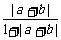 ≤
≤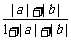 =
=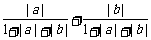 ≤
≤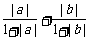 .
.
法2:分析法
当|a+b|=0时,不等式成立;
当|a+b|≠0时,原不等式即为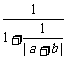 ≤
≤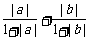 .
.
∵|a+b|≤|a|+|b|,
∴左边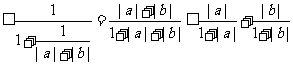
(2)(综合法)由已知得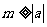 ,
,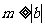 ,
,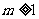 ,
,
从而知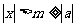 ,
, 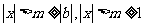

7.解不等式
(1) |x2─3|x|─3|£1; (2)|x-x2-2|>x2-3x-4 (x>-3)
解:(1) ∵|x2─3|x|─3|£1
∴─1£x2─3|x|─3£1
∴ Þ
Þ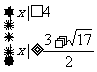
∴ 原不等式的解是: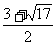 £x£4或─4£x£
£x£4或─4£x£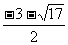
点评:本题由于运用了x∈R时,x2=|x|2从而避免了一场大规模的讨论
(2)法1:原不等式等价于:x-x2-2<-(x2-3x-4) ①
或:x-x2-2>x2-3x-4 ②
解①得:x>1, 解②得: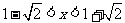
∴原不等式的解集为: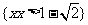 .
.
法2: ……
……
5. {x|1≤x≤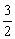 或
或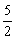 ≤x≤3 }; 6. 6. ①②④
≤x≤3 }; 6. 6. ①②④
[解答题]
6.已知|a+b|<-c(a、b、c∈R),给出下列不等式:
①a<-b-c;②a>-b+c;③a<b-c;④|a|<|b|-c;⑤|a|<-|b|-c.
其中一定成立的不等式是____________.(把成立的不等式的序号都填上)
简答:1-4. BDAB; 4.|x-4|+|x-3|表示数轴上的点x到(4, 0)与(3, 0)两点距离和,最小值为1,∴当a>1时,不等式有解.
5.不等式1≤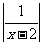 ≤2的解集是
≤2的解集是

4.不等式|x-4|+|x-3|<a有解的充要条件是( )
A.a>7 B.a>1 C.a<1 D.a≥1
[填空题]
3.(2005山东)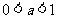 ,下列不等式一定成立的是( )
,下列不等式一定成立的是( )
A.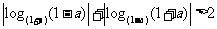
B.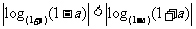
C.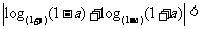
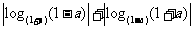
D.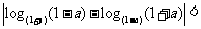
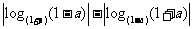
2.不等式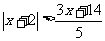 的解集是 ( )
的解集是 ( )
A.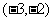 B.
B.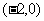 C.
C.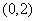 D.
D.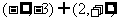
1.若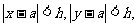 则下列不等式一定成立的是( )
则下列不等式一定成立的是( )
A.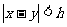 B.
B.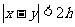 C.
C.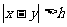 D.
D.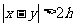
3、灵活运用绝对值不等式两个重要性质定理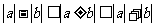 ,特别关注等号成立的条件。
,特别关注等号成立的条件。
同步练习 6.6含绝对值的不等式
[选择题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com