
灵感是一种直觉思维.它大体是指由于长期实践,不断积累经验和知识而突然产生的富有创造性的思路和思维闪光点.它是认识上质的飞跃,灵感的发生往往伴随着突破和创新.
在教学中,教师应及时捕捉和诱发学生学习中出现的灵感,对于学生别出心裁的想法,违反常规的解答,标新立异的构思,哪怕只有一点点的新意,都应及时给予肯定.同时,还应当运用数形结合、变换角度、类比形式等方法诱导学生数学直觉和灵感,促使学生能直接越过逻辑推理而寻找到解决问题的突破口.
发散思维是指从同一原材料探求不同答案的过程.它具有流畅性、变通性和创造性的特征.加强发散思维能力的训练,是培养学生创造思维的重要环节.根据现代心理学的观点,一个人创造能力的大小,一般来说与他的发散思维能力是成正比例的.
在教学中,培养学生的发散思维能力一般可以从以下几个方面入手.训练学生对同一条件,联想多种结论;改变思维角度,进行变式训练;培养学生个性,鼓励创优创新;加强一题多解、一题多变、一题多思等.特别是近年来,随着开放题的出现,不仅弥补了以往习题发散思维的不足,同时也为发散思维注入新
的活力.
想象是思维探索的翅膀. 爱因斯坦说:“想象比知识更重要,因为知识是有限的,而想象可以包括整个宇宙.”在教学中,引导学生进行数学想象,往往能缩短解决问题的时间,获得数学发现的机会,锻炼数学思维品质.
想象不同于胡思乱想. 数学想象一般有以下几个基本要素. 第一,因为想象往往是一种知识飞跃性的联结,因此,要有扎实的基础知识和丰富经验的支持.第二,要有能迅速摆脱表象干扰的敏锐的洞察力和丰富的识别力. 第三,要有执着追求的情感. 因此,培养学生的想象力,首先要使学生学好有关的基础知识. 其次,新知识的产生除去推理外,常常包含前人的想象因素. 因此,在教学中应根据教材潜在的因素,创设想象情境,提供想象材料,诱发学生的创造性想象. 另外,还应指导学生掌握一些想象的方法,如类比、归纳等.著名的哥德巴赫猜想就是通过归纳提出来的,而仿生学的诞生,则是类比联想的典型事例.
观察是信息输入的通道,是思维探索的大门. 敏锐的观察力是创造性思维的起步器,可以说没有观察就没有发现,更不会有创造. 学生的观察力是在学习过程中实现的,在课堂中,怎样培养学生的观察力呢?
首先,要给学生提出明确而具体的目的、任务和要求. 其次,要在观察中及时指导. 比如要指导学生选择适当的观察方法,要指导学生有顺序地进行观察,要指导学生及时地对观察的结果进行分析总结等. 再次,要科学的运用直观教具及现代教学技术,以支持学生仔细、深入地观察. 最后,要培养学生浓厚的观察兴趣.
17.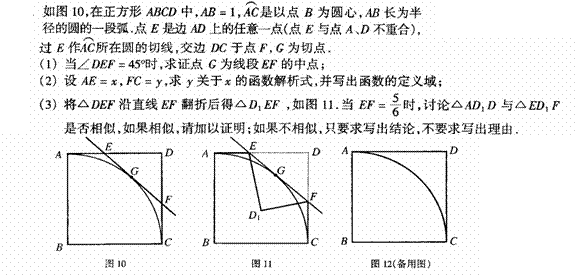
16.如图,已知⊙O1经过⊙O2的圆心O2,且与⊙O2相交于A、B两点,点C为弧AO2B上的一动点(不运动至A、B),连结AC,并延长交⊙O2于点P,连结BP、BC.
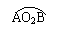 ⑴先按题意将图1补完整,然后操作,观察.图1供操作观察用,操作时可使用量角器与刻度尺,当点C在 上运动时,图中有哪些角的大小没有变化.
⑴先按题意将图1补完整,然后操作,观察.图1供操作观察用,操作时可使用量角器与刻度尺,当点C在 上运动时,图中有哪些角的大小没有变化.
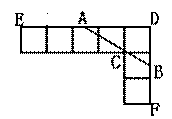
⑵请猜想△BCP的形状,并证明你的猜想(图2供证明用).
⑶如图3,当PA经过点O2时,AB=4,BP交⊙O1于D,且PB、DB的长是方程x2+kx+10=0的两个根,求⊙O1的半径.

15.如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.
⑴若DA =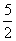 ,求DB的长;
,求DB的长;
⑵若DA、DB是方程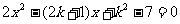 的两根,求
的两根,求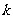 的值;
的值;
⑶估计AB的长度的范围.
14.
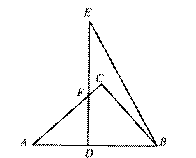
13. 要使图中平面展开图按虚线折叠成正方体后,相对面上
两个数之和为6,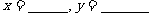 ;
;
12.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com