
22.在各项为正的数列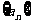 中,数列的前n项和
中,数列的前n项和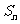 满足
满足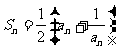
(1) 求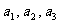 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列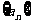 的通项公式;(3) 求
的通项公式;(3) 求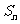
21.设平面内有n条直线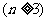 ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用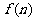 表示这n条直线交点的个数,则
表示这n条直线交点的个数,则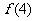 =
;
=
;
当n>4时,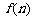 =
(用含n的数学表达式表示)
=
(用含n的数学表达式表示)
20.函数y=f(x)在(0,2)上是增函数,函数y=f(x+2)是偶函数,则f(1),f(2.5),f(3.5)的大小关系是 .
19.从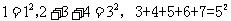 中,可得到一般规律为 (用数学表达式表示)
中,可得到一般规律为 (用数学表达式表示)
18. 类比平面几何中的勾股定理:若直角三角形ABC中的两边AB、AC互相垂直,则三角形三边长之间满足关系: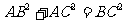 。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为
.
。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为
.
17.△ABC三边长
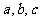 的倒数成等差数列,求证:角
的倒数成等差数列,求证:角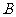
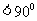 .
.
第Ⅱ卷(共50分)
16. 已知函数
已知函数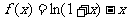 ,求
,求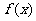 的最大值.
的最大值.
15.已知:空间四边形ABCD中,E,F分别为BC,CD的中点,判断直线EF与平面ABD的关系,并证明你的结论.
14.在△ABC中,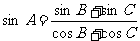 ,判断△ABC的形状.
,判断△ABC的形状.
13.证明: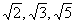 不能为同一等差数列的三项.
不能为同一等差数列的三项.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com