
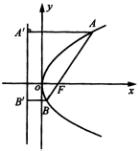
1、设双曲线  的左准线与
的左准线与
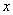 轴的交点是
轴的交点是
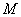 ,则过点
,则过点
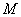 与双曲线
与双曲线
 有且只有一个交点的直线共有(
)
有且只有一个交点的直线共有(
)
A. 2条 B. 3条 C. 4条 D. 无数条
6、过椭圆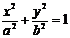 (a>b>0)左焦点的焦点弦为AB,则
(a>b>0)左焦点的焦点弦为AB,则 ,过右焦点的弦
,过右焦点的弦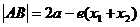 ;
;
[典型例题]
例1. 已知椭圆 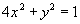 及直线
及直线
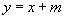 .
.
(1)当  为何值时,直线与椭圆有公共点?
为何值时,直线与椭圆有公共点?
(2)若直线被椭圆截得的弦长为 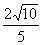 ,求直线的方程.
,求直线的方程.
分析:直线与椭圆有公共点,等价于它们的方程组成的方程组有解. 因此,只须考虑方程组消元后所得的一元二次方程的根的判别式. 已知弦长,由弦长公式就可求出  .
.
解:(1)把直线方程 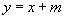 代入椭圆方程
代入椭圆方程
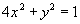 得
得
 ,即
,即 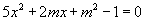 .
.
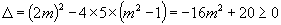 ,
,
解得  .
.
(2)设直线与椭圆的两个交点的横坐标为 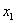 ,
,
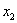 ,
,
由(1)得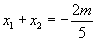 ,
,
 .
.
根据弦长公式得
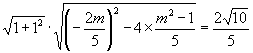 .
.
解得  .
.
因此,所求直线的方程为 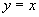 .
.
说明:处理有关直线与椭圆的位置关系问题及有关弦长问题,采用的方法与处理直线和圆的有所区别. 这里解决直线与椭圆的交点问题,一般考虑判别式 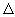 ;解决弦长问题,一般应用弦长公式. 用弦长公式,若能合理运用韦达定理(即根与系数的关系),可大大简化运算过程.
;解决弦长问题,一般应用弦长公式. 用弦长公式,若能合理运用韦达定理(即根与系数的关系),可大大简化运算过程.
例2. 直线  与双曲线
与双曲线
 相交于
相交于
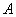 、
、
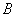 两点. 当
两点. 当  为何值时,以
为何值时,以
 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.
解:由方程组: 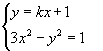 得
得
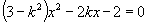
因为直线与双曲线交于 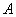 、
、
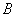 两点
∴
两点
∴ 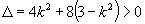
解得 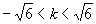 .
.
设  ,
,
 ,则:
,则:
 ,
,
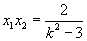 ,
,
而以  为直径的圆过原点,则
为直径的圆过原点,则
 ,
,
∴  .
.
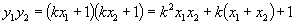 .
.
于是 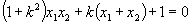 ,
,
即 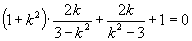 .
.
解得  满足条件.
满足条件.
故当  时,以
时,以
 为直径的圆过原点.
为直径的圆过原点.
例3. 斜率为1的直线经过抛物线 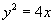 的焦点,与抛物线相交于两点
的焦点,与抛物线相交于两点
 、
、
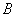 ,求线段
,求线段
 的长。
的长。
解:由抛物线的标准方程可知,焦点 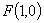 ,准线方程
,准线方程
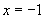 .
.
由题设,直线  的方程为:
的方程为:
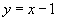 .
.
代入抛物线方程 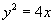 ,整理得:
,整理得:
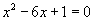 .
.
解法一:解上述方程得:  ,
,
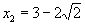
分别代入直线方程得: 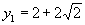

即  坐标分别为
坐标分别为
 、
、
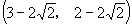 .
.
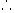
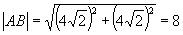
解法二:设  ,
,
 ,则:
,则:

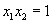
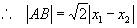
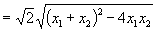
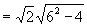
=8
解法三:设  、
B(x2,y2). 由抛物线定义可知,
、
B(x2,y2). 由抛物线定义可知,  等于点
等于点
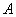 到准线
到准线
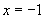 的距离
的距离
 .
.
即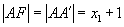
同理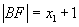
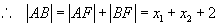
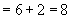
点拨:(1)解法一利用传统的基本方法求出  两点坐标,再利用两点间距离公式求出
两点坐标,再利用两点间距离公式求出
 的长。解法二没有利用直线求出
的长。解法二没有利用直线求出
 坐标。而是利用韦达定理找到
坐标。而是利用韦达定理找到
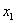 与
与
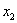 的关系,利用直线截二次曲线的弦长公式
的关系,利用直线截二次曲线的弦长公式
 求得,这是典型的设而不求思想方法比解法一先进,解法三充分利用抛物线的定义,把过焦点的这一特殊的弦分成两个半径的和,转化为准线的距离,这是思维质的飞跃。
求得,这是典型的设而不求思想方法比解法一先进,解法三充分利用抛物线的定义,把过焦点的这一特殊的弦分成两个半径的和,转化为准线的距离,这是思维质的飞跃。
(2)抛物线 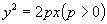 上一点
上一点
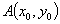 到焦点
到焦点
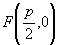 的距离
的距离
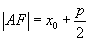 这就是抛物线的焦半径公式。焦点弦长
这就是抛物线的焦半径公式。焦点弦长
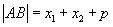
例4. 若直线 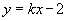 与抛物线
与抛物线
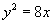 交于A、B两点,且AB中点的横坐标为2,求此直线方程.
交于A、B两点,且AB中点的横坐标为2,求此直线方程.
分析:由直线与抛物线相交利用韦达定理列出k的方程求解. 另由于已知与直线斜率及弦中点坐标有关,故也可利用“作差法”求k.
解法一:设 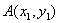 、
、
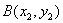 ,则由:
,则由:

可得: 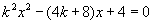
∵直线与抛物线相交,
 且
且 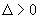 ,则
,则
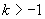
∵AB中点横坐标为: 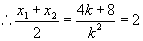
解得: 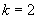 或
或
 (舍去)
(舍去)
故所求直线方程为: 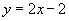
解法二:设 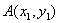 、
、
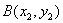 ,则有
,则有
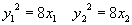
两式作差解:  ,
,
即 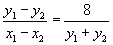
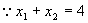
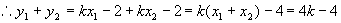
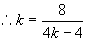
故 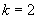 或
或
 (舍去)
(舍去)
则所求直线方程为: 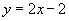
例5. (1)设抛物线
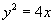 被直线
被直线
 截得的弦长为
截得的弦长为
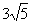 ,求k值.
,求k值.
(2)以(1)中的弦为底边,以x轴上的点P为顶点作三角形,当三角形的面积为9时,求P点坐标.
分析:(1)题可利用弦长公式求k,(2)题可利用面积求高,再用点到直线距离求P点坐标.
解:(1)由 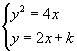 得:
得:
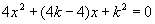
设直线与抛物线交于 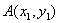 与
与
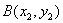 两点. 则有:
两点. 则有:
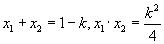
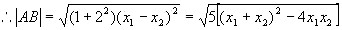

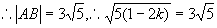 ,即
,即 
(2)  ,底边长为
,底边长为
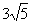 ,
,
∴三角形高 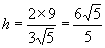
∵点P在x轴上,∴设P点坐标是 
则点P到直线 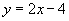 的距离就等于h,即
的距离就等于h,即 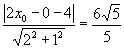
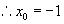 或
或 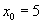 ,
,
即所求P点坐标是(-1,0)或(5,0).
[模拟试题]
5、抛物线y2=2px(p>0)的焦点弦(过焦点的弦)为AB,A(x1,y1)、B(x2,y2),则有如下结论:(1)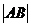 =x1+x2+p;(2)y1y2=-p2,x1x2=
=x1+x2+p;(2)y1y2=-p2,x1x2= ;
;
4、椭圆、双曲线的通径(最短弦)为 ,焦准距为p=
,焦准距为p= ,抛物线的通径为2p,焦准距为p; 双曲线
,抛物线的通径为2p,焦准距为p; 双曲线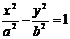 (a>0,b>0)的焦点到渐近线的距离为b;
(a>0,b>0)的焦点到渐近线的距离为b;
3. 已知弦AB的中点,研究AB的斜率和方程。
(1)AB是椭圆 (
(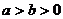 )的一条弦,中点M坐标为
)的一条弦,中点M坐标为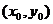 ,则AB的斜率为
,则AB的斜率为 ,运用点差法求AB的斜率,设
,运用点差法求AB的斜率,设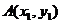 ,
, 。A、B都在椭圆上,
。A、B都在椭圆上,
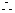
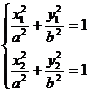 ,
,
两式相减得 。
。
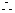
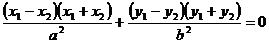 ,
,
即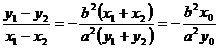 。故
。故 。
。
(2)运用类比的手法可以推出,已知AB是双曲线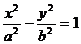 的弦,中点
的弦,中点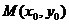 ,则
,则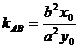 ;
;
(3)已知抛物线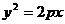 (
( )的弦AB的中点
)的弦AB的中点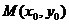 ,则
,则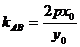 。
。
2. 连结圆锥曲线上的两点的线段称为圆锥曲线的弦。
直线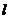 :
: ,曲线
,曲线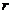 :
: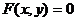 ,
,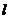 与
与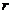 的两个不同的交点A、B,
的两个不同的交点A、B,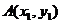 ,
, ,则
,则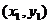 ,
, 是方程组
是方程组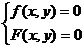 的两组解,方程组消元后化为关于
的两组解,方程组消元后化为关于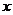 (或者
(或者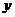 )的一元二次方程
)的一元二次方程 (
( ),判别式
),判别式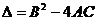 ,应有
,应有 ,所以
,所以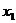 、
、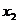 是方程
是方程 的解,由根与系数的关系(韦达定理)求出
的解,由根与系数的关系(韦达定理)求出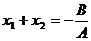 ,
,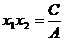 。所以A、B两点间距离为
。所以A、B两点间距离为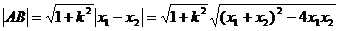 ,即弦长公式。也可以写成关于
,即弦长公式。也可以写成关于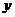 的形式,其弦长公式为
的形式,其弦长公式为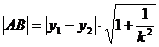 。
。
1. 判断直线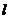 与圆锥曲线
与圆锥曲线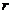 的位置关系时,通常将直线
的位置关系时,通常将直线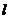 的方程
的方程 (A、B不同时为0)代入圆锥曲线
(A、B不同时为0)代入圆锥曲线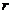 的方程
的方程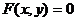 。消去
。消去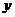 (也可以消去
(也可以消去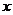 )得到一个关于变量
)得到一个关于变量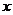 (或者变量
(或者变量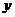 )的一元二次方程。
)的一元二次方程。
即 ,消去
,消去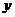 后的
后的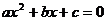 。
。
(1)当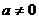 时,则有
时,则有 ,直线
,直线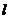 与曲线
与曲线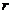 相交;
相交;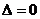 ,直线
,直线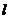 与曲线
与曲线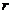 相切;
相切; ,直线
,直线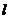 与曲线
与曲线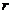 相离。
相离。
(2)当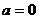 时,即得到一个一次方程,则
时,即得到一个一次方程,则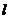 与
与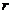 相交,且只有一个交点,此时,若
相交,且只有一个交点,此时,若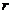 为双曲线,则直线
为双曲线,则直线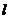 与双曲线的渐近线是平行;若
与双曲线的渐近线是平行;若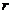 为抛物线,则直线
为抛物线,则直线 与抛物线的对称轴的位置关系是平行。
与抛物线的对称轴的位置关系是平行。
掌握直线与圆锥曲线的位置关系的判断方法,能够正确熟练地解决与直线和圆锥曲线的位置关系相关的一些问题。这类问题常涉及到圆锥曲线的性质和直线的基本知识点、线段的中点、弦长、垂直问题,因此分析问题时利用数形结合思想和设而不求法与弦长公式及韦达定理联系去解决。
圆锥曲线与直线的位置关系
10、想像:在原有的感性形象的基础上,创造新形象的心理过程。
作用:为塑造形象、表现主题服务。使读者接受美的陶冶。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com