
20.(本小题满分14分)
一个不透明的口袋内装有材质、重量、大小相同的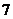 个小球,且每个小球的球面上要么只写有数字“
个小球,且每个小球的球面上要么只写有数字“ ”,要么只写有文字“世博会” .假定每个小球每一次被取出的机会都相同,又知从中摸出
”,要么只写有文字“世博会” .假定每个小球每一次被取出的机会都相同,又知从中摸出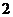 个球都写着“世博会”的概率是
个球都写着“世博会”的概率是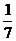 .现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有一人取得写着文字“世博会”的球时游戏终止.
.现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有一人取得写着文字“世博会”的球时游戏终止.
(1)求该口袋内装有写着数字“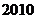 ”的球的个数;
”的球的个数;
(2)求当游戏终止时总球次数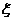 的概率分布列和期望E
的概率分布列和期望E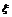 .
.
19.(本小题满分14分)
 的展开式中各项的二项式系数之和为
的展开式中各项的二项式系数之和为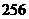 .
.
(1)求展开式中各项系数之和;
(2)求展开式中含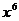 的项;
的项;
(3)求展开式中系数的绝对值最大的项.
18.(本小题满分10分)
已知矩阵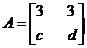 ,若矩阵
,若矩阵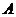 属于特征值
属于特征值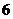 的一个特征向量为
的一个特征向量为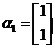 ,属于特征值
,属于特征值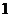 的一个特征向量为
的一个特征向量为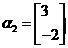 .
.
(1)求矩阵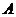 ,并写出
,并写出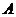 的逆矩阵;
的逆矩阵;
(2)若向量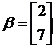 ,试计算
,试计算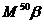 .
.
(选修4-5:不等式选讲)
已知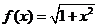 是定义在区间
是定义在区间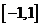 上的函数,设
上的函数,设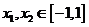 且
且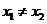 .
.
(1)求证: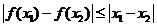 ;
;
(2)若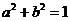 ,求证:
,求证: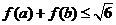 .
.
17.(本小题满分10分)
已知命题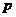 :
: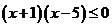 ,命题
,命题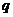 :
: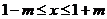 (
( ).
).
(1)若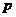 是
是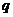 的充分条件,求实数
的充分条件,求实数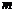 的取值范围;
的取值范围;
(2)若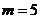 ,“
,“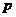 或
或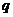 ”为真命题,“
”为真命题,“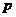 且
且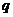 ”为假命题,求实数
”为假命题,求实数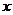 的取值范围.
的取值范围.
16.(本小题满分10分)
设等比数列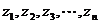 ,其中
,其中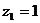 ,
,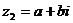 ,
,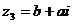
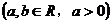 .
.
(1)求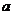 ,
,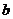 的值;
的值;
(2)若等比数列的公比为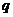 ,且复数
,且复数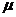 满足
满足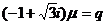 ,求
,求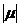 .
.
15.(本小题满分10分)
已知曲线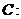
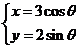 ,直线
,直线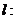
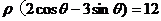 .
.
(1)将直线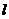 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)设点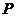 在曲线
在曲线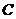 上,求
上,求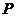 点到直线
点到直线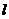 的距离的最小值.
的距离的最小值.
14. 观察下列算式:
观察下列算式:
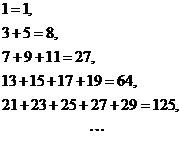
猜测第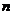 行的式子为 ▲
.
行的式子为 ▲
.
13.下列命题中:
① 若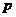 、
、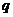 为两个命题,则“
为两个命题,则“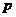 且
且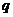 为真”是“
为真”是“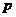 或
或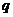 为真”的必要不充分条件;
为真”的必要不充分条件;
② 若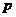 为:
为: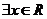 ,
,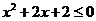 ,则
,则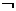
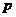 为:
为: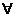
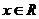 ,
,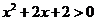 ;
;
③若命题“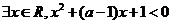 ”是假命题,则实数
”是假命题,则实数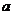 的取值范围是
的取值范围是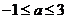 ;
;
④ 已知命题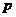 :
: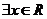 ,使
,使 ,命题
,命题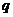 :
: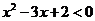 的解集是
的解集是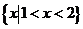 ,则命题
,则命题
“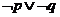 ”是假命题.
”是假命题.
所有正确命题的序号是 ▲ .
12.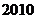 年上海世博会大力倡导绿色出行,并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量.某游客非常支持这一方案,计划在游园期间种植某种树,已知这种树的的成活率为
年上海世博会大力倡导绿色出行,并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量.某游客非常支持这一方案,计划在游园期间种植某种树,已知这种树的的成活率为 ,设
,设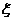 表示他所种植的树成活与否,即
表示他所种植的树成活与否,即 ,
, 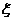 的方差为
的方差为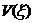 .则
.则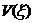 达到高@考#资$源@网最大值时
达到高@考#资$源@网最大值时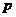 的值为 ▲ .
的值为 ▲ .
11.在平面内画一条直线,将平面分成两部分;画两条直线,最多将平面分成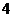 部分;画三条直线,最多将平面分成
部分;画三条直线,最多将平面分成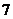 部分.那么平面内两两相交的
部分.那么平面内两两相交的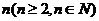 条直线,最多将平面分成 ▲
部分.
条直线,最多将平面分成 ▲
部分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com