6、球的截面性质：用一个平面截一个球面，所得截线是以　　　　　 为圆心，以r＝　　　　 为半径的一个圆，截面是一个　　　　　 ．

5、球的定义：　　　　　　　　　　　　 叫球体(简称球)，　　　　　　　　　　 叫球面．

4、正多面体的概念：____________________种类:_______________________________.

3、棱椎：

⑴棱锥：有一个面是_______________(底面)②其余各面都是有__________________(侧面).

正棱锥：底面____________② 顶点________________ 叫正棱锥

⑵棱椎的截面性质定理：_________________________.

⑶正棱锥的性质 ：①________________________②___________________________.

2、棱柱：

(1)棱柱的有关概念：　　　　　　　　 的多面体叫棱柱；　　　　　　　　　　　　 的

棱柱叫直棱柱；　　　　　　　　　　 的棱柱叫正棱柱；　　　　　　　　 叫平行六面体；

_______________________________叫长方体；　　　　　　　　　 的叫正方体.

(2)棱柱的分类：

①按侧棱与底面的位置关系分：侧棱不垂直于底面的棱柱叫斜棱柱，侧棱垂直于底面的棱柱叫直棱柱， 底面的是正多边形的直棱柱叫正棱柱。

　　　 ②按底面多边形的边数分：棱柱的底面可以是三角形、四边形、五边形……这样的棱柱分别叫三棱柱、四棱柱、五棱柱……

{正方体}⊊{长方体}⊊{直平行六面体}⊊{平行六面体}⊊{四棱柱}

(3)棱柱的性质：①___________________②___________________③__________________.

设长方体的长、宽、高分别为a、b、c，对角线长为l ，则l ²=a ²+b ²+c ²

(4)两个定理①______________________________；②_______________________________.

1、多面体：

____________________________________________________________________

11、二面角及二面角的平面角

(1)半平面　 直线把平面分成两个部分，每一部分都叫做半平面.

(2)二面角 　一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱，这两个平面叫做二面角的面，即二面角由半平面一棱一半平面组成.

二面角的平面角θ的取值范围是0°＜θ≤180°

　(3)二面角的平面角

①以二面角棱上任意一点为端点，分别在两个面内作垂直于棱的射线，这两条射线所组成的角叫做二面角的平面角.

如图，∠PCD是二面角α-AB-β的平面角.平面角∠PCD的大小与顶点C在棱AB上的位置无关.

②二面角的平面角具有下列性质：

(i)二面角的棱垂直于它的平面角所在的平面，即AB⊥平面PCD.

(ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线，垂足必在平面角的另一边(或其反向延长线)上.

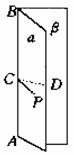(iii)二面角的平面角所在平面与二面角的两个面都垂直，即平面PCD⊥α，

平面PCD⊥β.

10、直线和平面所成的角

(1)定义　 和平面所成的角有三种：

(i)垂线 　面所成的角　 的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角.

(ii)垂线与平面所成的角　 直线垂直于平面，则它们所成的角是直角.

(iii)一条直线和平面平行，或在平面内，则它们所成的角是0°的角.

(2)取值范围：　　　　　　　　　

(3)求解方法

①作出斜线在平面上的射影，找到斜线与平面所成的角θ.

②解含θ的三角形，求出其大小.

9.空间中的各种角

等角定理及其推论

定理:若一个角的两边和另一个角的两边分别平行，并且方向相同，则这两个角相等.

推论:若两条相交直线和另两条相交直线分别平行，则这两组直线所成的锐角(或直角)相等.

异面直线所成的角

(1)定义：a、b是两条异面直线，经过空间任意一点O，分别引直线a′∥a,b′∥b,则a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角.

(2)取值范围：　　　　　　　　　 .

(3)求解方法

①根据定义，通过平移，找到异面直线所成的角θ；

②解含有θ的三角形，求出角θ的大小.

7.射影及有关性质

(1)点在平面上的射影自一点向平面引垂线，垂足叫做这点在这个平面上的射影，点的射影还是点.

(2)直线在平面上的射影自直线上的两个点向平面引垂线，过两垂足的直线叫做直线在这平面上的射影.

(4)射影的有关性质

从平面外一点向这个平面所引的垂线段和斜线段中：

(i)射影相等的两条斜线段相等，射影较长的斜线段也较长；

(ii)相等的斜线段的射影相等，较长的斜线段的射影也较长；

(iii)垂线段比任何一条斜线段都短.