
5.已知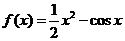 ,
,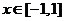 ,则导函数
,则导函数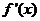 是( )
是( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
4.在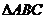 中,
中,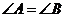 是
是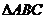 为等腰三角形的( )
为等腰三角形的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
3.两个变量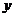 与
与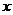 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数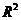 如下,其中拟合效果最好的模型是 (
)
如下,其中拟合效果最好的模型是 (
)
A.模型1的相关指数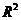 为
为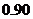 B.模型2的相关指数
B.模型2的相关指数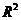 为
为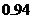
C.模型3的相关指数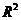 为
为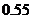 D.模型4的相关指数
D.模型4的相关指数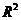 为
为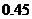
2.复数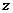 满足
满足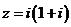 ,则
,则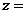 ( )
( )
A.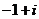 B.
B.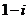 C.
C.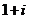 D.
D.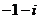
1.已知全集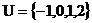 ,集合
,集合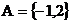 ,
,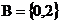 ,则
,则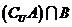 等于
(
)
等于
(
)
A.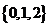 B.
B.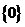 C.
C.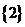 D.
D.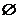
2、相对原子质量:
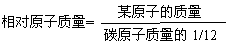 ⑴
⑴
⑵相对原子质量与原子核内微粒的关系:
相对原子质量 = 质子数 + 中子数
24.(本小题满分16分)
函数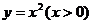 的图像在点
的图像在点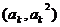 处的切线与
处的切线与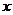 轴交点的横坐标为
轴交点的横坐标为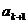 (
( 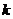 为正整数),其中
为正整数),其中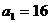 .设正整数数列
.设正整数数列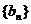 满足:
满足: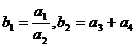 ,当
,当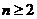 时,有
时,有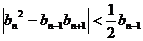 .
.
(Ⅰ) 求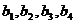 的值;
的值;
(Ⅱ)求数列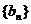 的通项;
的通项;
(Ⅲ) 记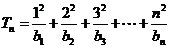 ,证明:对任意
,证明:对任意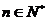 ,
,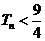 .
.
23.(本小题满分16分)
(1)已知实数集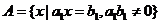 ,
,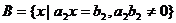 ,证明:
,证明: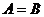 的充要条件是
的充要条件是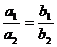 ;
;
(2)已知实数集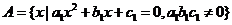 ,
,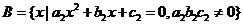 ,问
,问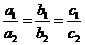 是
是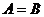 的什么条件?请给出说明过程;
的什么条件?请给出说明过程;
(3)已知实数集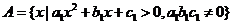 ,
,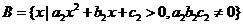 ,问
,问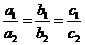 是
是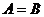 的什么条件?请给出说明过程.
的什么条件?请给出说明过程.
22.(本小题满分15分)
一个口袋中装有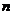 个红球(
个红球(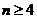 且
且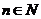 )和
)和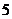 个白球,从中摸两个球,两个球颜色相同则为中奖.
个白球,从中摸两个球,两个球颜色相同则为中奖.
(Ⅰ)若一次摸两个球,试用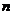 表示一次摸球中奖的概率
表示一次摸球中奖的概率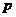 ;
;
(Ⅱ)若一次摸一个球,当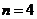 时,求二次摸球(每次摸球后不放回)中奖的概率;
时,求二次摸球(每次摸球后不放回)中奖的概率;
(Ⅲ)在(Ⅰ)的条件下,记三次摸奖(每次摸奖后放回)恰有二次中奖的概率为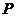 ,当
,当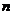 取多少时,
取多少时,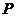 最大?
最大?
21.(本小题满分15分)
某出版公司为一本畅销书定价如下: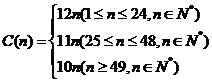 .这里
.这里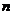 表示订购书的数量,
表示订购书的数量,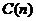 是订购
是订购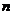 本书所付的钱数(单位:元).若一本书的成本价是
本书所付的钱数(单位:元).若一本书的成本价是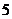 元,现有甲乙两人来买书,每人至少买
元,现有甲乙两人来买书,每人至少买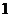 本,且乙买的书不少于甲买的书,两人共买
本,且乙买的书不少于甲买的书,两人共买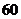 本.问出版公司至少能赚多少钱?最多能赚多少钱?
本.问出版公司至少能赚多少钱?最多能赚多少钱?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com