
8、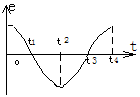 如图一矩形线圈绕垂直于匀强磁场并位于线圈平面内的固定轴转动,线圈中的感应电动势ε随时间t的变化如图所示,下面说法中正确的是( )
如图一矩形线圈绕垂直于匀强磁场并位于线圈平面内的固定轴转动,线圈中的感应电动势ε随时间t的变化如图所示,下面说法中正确的是( )
A.t1时刻通过线圈的磁通量为零
B.t2时刻通过线圈的磁通量的绝对值最大
C.t3时刻通过线圈的磁通量变化率的绝对值最大
D.每当e变换方向时,通过线圈的磁通量绝对值都为最大。
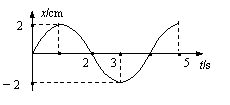
7、一个质点做简谐运动的图象如图所示,下述正确的是
A、质点振动频率为4赫兹
B、在前10 s内质点经过的路程是20 cm
C、在5 s末,速度为零,加速度最大
D、 t = 1.5 s和t = 4.5 s两时刻质点的速度相同,加速度相同
6、 如图所示,光滑水平面上停着一辆小车,小车的固定支架左端用不计质量的细线系一个小铁球.开始将小铁球提起到图示位置,然后无初速释放.在小铁球来回摆动的过程中,下列说法中正确的是( )
如图所示,光滑水平面上停着一辆小车,小车的固定支架左端用不计质量的细线系一个小铁球.开始将小铁球提起到图示位置,然后无初速释放.在小铁球来回摆动的过程中,下列说法中正确的是( )
A.小车和小球系统动量守恒
B.小球向右摆动过程小车一直向左加速运动
C.小球摆到右方最高点时刻,由于惯性,小车仍在向左运动
 D.小球摆到最低点时,小车的速度最大
D.小球摆到最低点时,小车的速度最大
4、某线圈在匀强磁场中转动所产生的电动势变化规律为e=ε sinωt,保持其它条件不变,使该线圈的转速和匝数同时增加一倍,则此时所产生的电动势的瞬时表达式将变为下述的:( )
sinωt,保持其它条件不变,使该线圈的转速和匝数同时增加一倍,则此时所产生的电动势的瞬时表达式将变为下述的:( )
A.e=2E sin2ωt
B.e=2E
sin2ωt
B.e=2E sinωt
C.e=4E
sinωt
C.e=4E sin2ωt
D.e=4E
sin2ωt
D.e=4E sinωt
sinωt
5、质量为m1=4kg、m2=2kg的A、B两球,在光滑的水平面上相向运动,若A球的速度为v1=3m/s,B球的速度为v2=-3m/s,发生正碰后,两球的速度的速度分别变为v1'和v2',则v1'和v2'可能为( )
A.v1'=1m/s,v2'=1m/s B.v1'=4m/s,v2'=-5m/s
C.v1'=2m/s,v2'=-1m/s D.v1'=-1m/s,v2'=5m/s
3、在学过《机械振动》、《机械波》后,四位同学就自己看到的现象,发表自己的观点,让你从物理学的角度来看,你认为他们谁说的对( )
小张说:医生用听诊器是利用了固体可以传递机械波
小王说:军队过桥时不能齐步走,就是因为怕产生共振,损坏了桥,火车过铁桥时要减速,也是同样的道理
小李说:我家的木板门,春夏季听不到响声,一到秋冬季节,就开始嘭嘭作响,这是风吹振动的
小赵说:树叶在水面上下振动说明,机械波并不向外传递介质
A.小张说的对 B.小王说的对 C.小李说的对 D.小赵说的对
2、从同一高度落下的玻璃杯掉在水泥地上易碎,掉在沙地上不易碎,这是因为玻璃杯落到水泥地上时( )
A.受到的冲量大 B.动量变化率大
C.动量改变量大 D.动量大
1、弹簧振子在振动过程中,每次通过同一位置时,都具有相同的( )
A.位移 B.速度
C.加速度 D.机械能
15(满分12分).
(1)证明:要证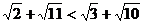 ,
,
需要证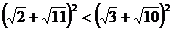 1分
1分
需证: 3分
3分
需证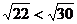 5分
5分
因为22<30 所以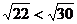 ,
,
故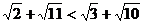 .
6分
.
6分
(2)证明: 要证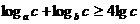
需证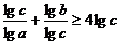 7分
7分
由于c>1,只需要证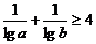 8分
8分
即证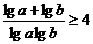 需证
需证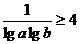
需证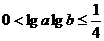 9分
9分
由于ab=10, 则lgab=1即lga+lgb=1
而a,b均为大于1 的数,即lga>0
且lgb>0,则lga+lgb≥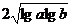
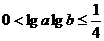 11分
11分
故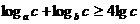 12分
12分
16(满分12分)解:(1)将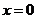 ,
,
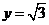 代入函数
代入函数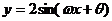 得
得
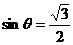 ,因为
,因为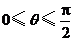 ,所以
,所以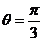 . 3分
. 3分
又因为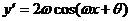 ,
,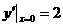 ,
,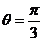 ,所以
,所以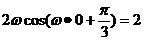
即 ,
6分
,
6分
(2),由(1)知 .
.
由五点法作图知,即当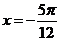 时,当
时,当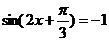 ,取
,取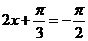 ,得
,得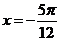 (8分)
(8分)
由于 周期为
周期为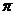 即把
即把 图像向右平移
图像向右平移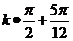
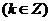 单位时,得到函数的图像都关于y轴对称。
单位时,得到函数的图像都关于y轴对称。
即m=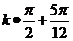
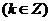 10分
10分
由于m>0,故m的最小值为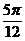 12分
12分
17(满分14分).
(1)证法一:取BE中点N,连MN,AN,则MN为三角形BCE中位线,所以
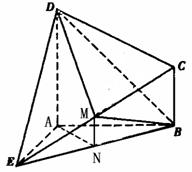 MN//BC,又∵AD//BC,
MN//BC,又∵AD//BC,
∴MN//AD,故D、M、N、A共面, 2分
又AD⊥平面ABE,∴MN⊥平面ABE,
又∵BE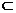 平面ABE,∴MN⊥BE
3分
平面ABE,∴MN⊥BE
3分
又∵AE=AB,所以AN为等要直角三角形BAE底边BE上的高,即AN⊥BE
又∵AD∩NM=N
∴BE⊥平面ANMD 4分
又DM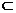 平面ANMD
平面ANMD
∴BE⊥DM。 5分
证法二:建立如图所示的空间直角坐标系并设EA=DA=AB=2CB=2
则D(0,0,2)、C(0,2,1),
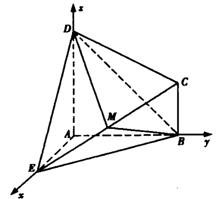 B(0,2,0),E(2,0,0),M(1,1,
B(0,2,0),E(2,0,0),M(1,1,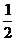 )。
)。
(1)
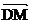 =(1,1,-
=(1,1,-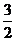 ),
),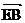 =(-2,2,0) (3分)
=(-2,2,0) (3分)
因为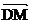

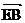 =0从而得DM
=0从而得DM EB (5分)
EB (5分)
(2) 解法一:设n1=(x,y,z)是平面BDM的法向量。
则由n1
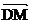 ,
n1
,
n1
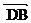 及
及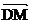 =(1,1,-
=(1,1,-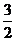 ),
),
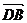 =(0,2,-2)
=(0,2,-2)
得:
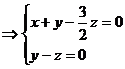
可以取x=1,则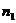 =(1,2,2)。
(10分)
=(1,2,2)。
(10分)
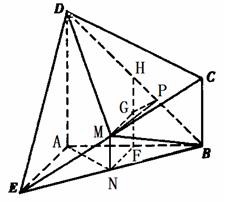 显然,n2=(1,0,0)为平面BDM的法向量。
(12分)
显然,n2=(1,0,0)为平面BDM的法向量。
(12分)
设二面角M-BD-A的平面角为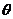 ,则此二面角余弦值
,则此二面角余弦值
cos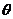 =
=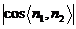 =
=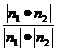 =
=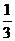 (14分)
(14分)
解法二:取AB中点F,取BD中点H,连NF,FH
由于FH为三角形DAB的中位线,所以FH//AD
所以HF⊥平面ABE,结合MN⊥平面ABE
则FH//MN 6分
又NF为三角形BAE的中位线,所以NF//AE
容易证明:EA⊥平面ABD
NF⊥平面ABD 7分
过M作MG⊥平面ABD,则BD⊥GM,
且垂足必然在FH上,过G作GP⊥BD交于P点
又∵MG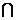 GP=G
GP=G
∴BD⊥平面MGP ,MP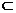 平面MGP
平面MGP
∴BD⊥MP∠GPM为二面角M-BD-A的平面角。 9分
不妨设EA=DA=AB=2CB=4
由以上证明可知道NMGF为矩形,所以MG=NF=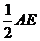 =2,
=2,
MN为三角形BCE中位线,所以MN=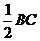 =1,即FG=NM=1
10分
=1,即FG=NM=1
10分
由于FH=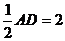 =BC且HF⊥AB,BC⊥AB,所以BCHF为正方形,则FC⊥BH
=BC且HF⊥AB,BC⊥AB,所以BCHF为正方形,则FC⊥BH
FG=1=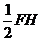 ,所以G为FH中点,则
,所以G为FH中点,则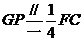 =
=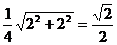 12分
12分
∴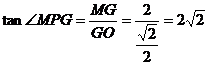 ,
,
∴ 14分
14分
18(满分14分).解:(1) f(x)-2是奇函数,
f(x)-2是奇函数,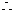 f(-x)-2= -
f(-x)-2= -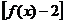 ,
,
 f(x)=ax3+bx2+cx+d,∴-ax3+bx2-cx+d-2=-ax3-bx2-cx-d+2, ∴bx2+d-2=0,
f(x)=ax3+bx2+cx+d,∴-ax3+bx2-cx+d-2=-ax3-bx2-cx-d+2, ∴bx2+d-2=0,
 x
x R, ∴b=0,d=2,
(2分)
R, ∴b=0,d=2,
(2分)
∴f(x)=ax3+cx+2,∴f’(x)=3ax2+c
 f(x)在x= -1处取得极大值,
f(x)在x= -1处取得极大值,
∴f’(-1)=0,∴3a+c=0, ∴c=-3a 3分
又 直线l:x-3y+1=0的斜率为
直线l:x-3y+1=0的斜率为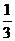 ,f(x)的图像在原点处的切线与直线l垂直。
,f(x)的图像在原点处的切线与直线l垂直。
∴f’(0)= -3,c= -3 ∴a=1, 5分
∴ f’(x)=3x2-3=3(x-1)(x+1),
 当x<-1时,f(x)=x3-3x+2。f’(x)>0,当-1<x<1时,f’(x) <0,
当x<-1时,f(x)=x3-3x+2。f’(x)>0,当-1<x<1时,f’(x) <0,
∴f(x)在x= -1处取得极大值,符合题意。
∴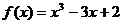 7分
7分
(2)由(1)知f(x)=ax3-3ax+2,f’(x)=3ax2-3a=3a(x-1)(x+1), 8分
令f’(x)=0,得x=1或x= -1。
 f(x)在x= -1处取得极大值,
9分
f(x)在x= -1处取得极大值,
9分
∴当x< -1时,f’(x)>0.当-1<a<1时,f’(x)<0,
∴a>0. 10分
当x
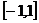 时,不等式f(x)
时,不等式f(x)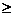 0恒成立等价于f(x)min
0恒成立等价于f(x)min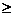 0,
11分
0,
11分
 f(x)在
f(x)在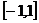 上是减函数,∴ f(x)的最小值为f(1),
12分
上是减函数,∴ f(x)的最小值为f(1),
12分
∴f(1)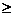 0,∴
2-2a
0,∴
2-2a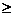 0,∴ a
0,∴ a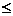 1。
13分
1。
13分
综上所述,a的取值范围是0<a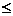 1。
14分
1。
14分
19(满分14分).解:(1)设P(x,y),依题意,有
k
 k
k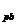 =
=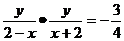 (
(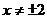 )
(2分)
)
(2分)
化简得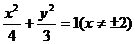 ,这就是动点P的轨迹C的方程
(5分)
,这就是动点P的轨迹C的方程
(5分)
说明:没写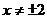 扣1分。
扣1分。
(2)解法一:依题意,可设M(x,y)、E(x+m,y+n)、F(x-m,y-n),
则有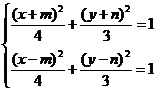 (6分)
(6分)
两式相减,得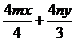 =0 得到kEF=
=0 得到kEF=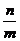 =
=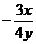 =
=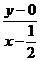 ,
(8分)
,
(8分)
由此得点M的轨迹方程为6x2+8y2-3x=0(x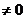 )
(10分)
)
(10分)
设直线MA:x=qy+2(其中q= ),
),
则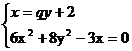 得到(6q2+8)y2+21qy+18=0
(12分)
得到(6q2+8)y2+21qy+18=0
(12分)
故由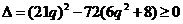 得出
得出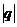
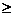 8,即
8,即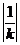
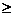 8,
8,
解之得k的取值范围是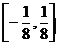 。
(14分)
。
(14分)
解法二:当过点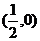 垂直于x轴的直线
垂直于x轴的直线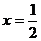 ,与椭圆
,与椭圆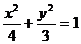 相交的两点EF中点显然为
相交的两点EF中点显然为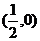 ,∴
,∴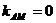 ,说明0是所求范围内的一个值。
(6分)
,说明0是所求范围内的一个值。
(6分)
当直线过点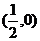 不垂直x轴时设直线AEFM方程为
不垂直x轴时设直线AEFM方程为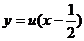 ,
,
代入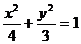 并整理得
并整理得
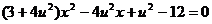 (*)
(*)
由于过椭圆内一点作直线与椭圆必然相交,所以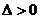 ,设
,设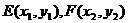 ,M(x,y)
,M(x,y)
那么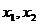 是方程(*)的两根,由韦达定理得
是方程(*)的两根,由韦达定理得
 则
则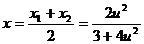 ①
①
又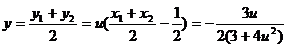 ②
( 8分)
②
( 8分)
①÷②得到: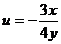 ,又∵
,又∵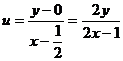 ( 9分)
( 9分)
∴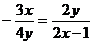
由此得点M的轨迹方程为6x2+8y2-3x=0(x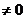 )
(10分)
)
(10分)
以下解法同解法一.
解法三:由解法二知道: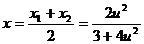 ;
;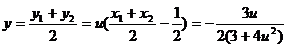
那么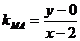
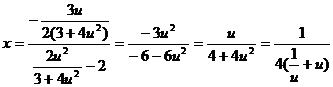
当u>0时,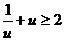
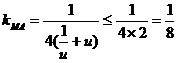
当u<0时,∵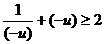 ,∴
,∴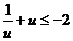
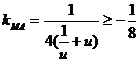
故: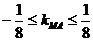
说明:(1)本题第(2)小问解法一利用点差法时,设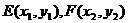 代入椭圆方程,求EF中点(x,y)的轨迹方程请给出相应分数
代入椭圆方程,求EF中点(x,y)的轨迹方程请给出相应分数
(2) 第(2)小问解法中,若没有讨论直线斜率不存在而直接设直线MA方程为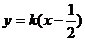 求解,扣1分.
求解,扣1分.
20(满分14分).解析:(1)若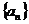 为常数列,则an=a由an+1=f(an),
为常数列,则an=a由an+1=f(an),
得:a=f(a) (1分)

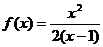 ,
,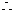
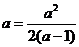 ,
,
 a>1,
a>1,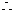 a=2(a-1),解得:a=2
(4分)
a=2(a-1),解得:a=2
(4分)
(2)当a=2时,有(1)知an=2; (5分)
当a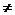 2时,
2时, a1=a,an+1=
a1=a,an+1=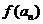 =
=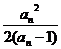 ,∴ a2=
,∴ a2=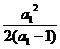 =
=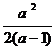 ,
,
∴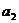 -2=
-2=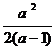 -2=
-2=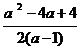 =
=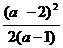 >0,∴ a2>2,
(6分)
>0,∴ a2>2,
(6分)
 a3-2=
a3-2=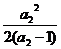 -2=
-2=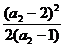 >0,
>0,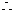 a3>2,猜想当n
a3>2,猜想当n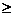 2时,an>2。 ( 7分)
2时,an>2。 ( 7分)
下面用数学归纳法证明:
1°当n=2时,a2>2,故猜想成立;
2°假设当n=k(k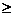 2)时,猜想成立,即ak>2,即当n=k+1时, (8分)
2)时,猜想成立,即ak>2,即当n=k+1时, (8分)
ak+1=f(ak)=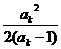 ,∴ak+1 - 2>
,∴ak+1 - 2>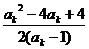 =
=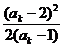 (9分)
(9分)
由1°2°可知,对于一切不小于2的正整数n都有an>2.
综上所述,当a=2时,an=2;
当1<a<2时,a1<2,an>2(n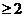 )
)
当a>2时,an>2. (10分)
(3)由an+1=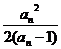 =
=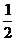 ×
×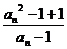 =
=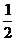 (an+1+
(an+1+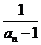 )
)
 当a>2时,an>2,
当a>2时,an>2,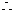
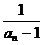 <1,
<1,
∴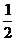 (an+1+
(an+1+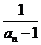 )<
)<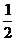 (an+1+1)=
(an+1+1)=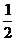 an+1,∴ an+1<
an+1,∴ an+1<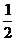 an+1
(11分)
an+1
(11分)
∴0 <an+1-2<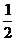 ( an-2),∴0<
( an-2),∴0<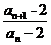 <
<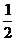 ,
(12分)
,
(12分)
∴an-2=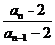 ×…×
×…×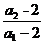 ×(a1-2)<(a1-2)(
×(a1-2)<(a1-2)(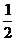 )n-1=(a-2)(
)n-1=(a-2)(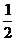 )n-1
)n-1
∴an<2+(a-2)(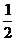 )n-1,
(13分)
)n-1,
(13分)
 2<a<3,
2<a<3,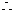 an<2+(
an<2+(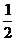 )n-1 ,
(14分)
)n-1 ,
(14分)
12.解法一:分两类第一类:两个节目相邻时,把两个节目插入原来5个节目所产生的6个空档中有: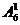 =6种方法,另外这两个节目本身互换有
=6种方法,另外这两个节目本身互换有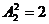 种,故有
种,故有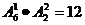
第二类:两个节目不相邻时,是把两个节目插入原来5个节目所产生的6个空档中有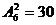 种,
种,
故有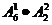 +
+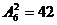 种。
种。
解法二:先把两个节目中的一个插入原来5个节目所产生的6个空档中有6种方法,再把剩下的一个节目插到6个节目所产生的7个空挡中有7种方法,故共有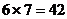 种方法。
种方法。
11.解法一:分三类:仅有两种服装,有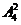 =12种种法;仅有三种服装,有
=12种种法;仅有三种服装,有 =48种种法;
=48种种法;
仅有四种服装,有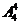 =24种种法.共有
=24种种法.共有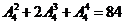 .
.
解法二:按区域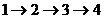 顺序着装,可分
顺序着装,可分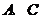 同色与不同色有
同色与不同色有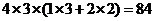
解法三:列出树状图如下:假设着装颜色分为A,B,C,D,四种,按区域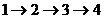 顺序着装
顺序着装
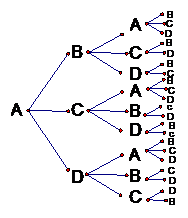
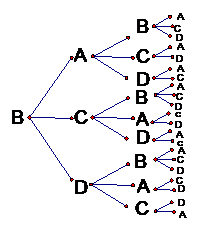
第一区着装为A颜色时,有21种 第一区着装为B颜色时,有21种
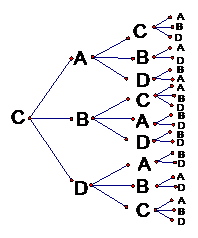
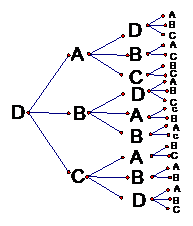
第一区着装为C颜色时,有21种; 第一区着装为D颜色时,有21种
共有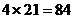 种
种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com