
1(广东卷)若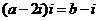 ,其中
,其中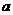 、
、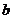
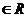 ,
,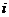 使虚数单位,则
使虚数单位,则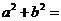
(A)0(B)2(C)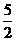 (D)5
(D)5
2. (福建卷)复数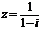 的共轭复数是
的共轭复数是
A.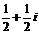 B.
B.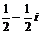 C.
C.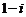 D.
D.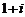
6.两个实数可以比较大小、但两个复数如果不全是实数,就不能比较它们的大小,
考试要求:
了解引进复数的必要性;理解复数的有关概念;掌握复数的代数表示及向量表示.
5、复平面:建立直角坐标系来表示复数的平面叫做复平面,x轴叫做实轴,y轴除去原点的部分叫虚轴.
4.共轭复数:当两个复数实部相等,虚部互为相反数时.这两个复数互为共轭复数。(当虚部不为零时,也可说成互为共轭虚数).
3.复数的相等:如果两个复数实部相等且虚部相等就说这两个复数相等,
2、分类:复数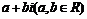 中,当时b=0,就是实数;当b
中,当时b=0,就是实数;当b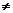 0时,叫做虚数;当a=0, b
0时,叫做虚数;当a=0, b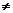 0时,叫做纯虚数
0时,叫做纯虚数
1、复数:形如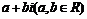 的数叫做复数,a,b分别叫它的实部和虚部.
的数叫做复数,a,b分别叫它的实部和虚部.
10. .已知A(4,0),N(1,0),若点P满足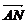 ·
·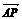 =6|
=6|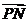 |.
|.
(1)求点P的轨迹方程,并说明该轨迹是什么曲线;
(2)求|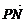 |的取值范围;
|的取值范围;
解:(1)设P(x,y),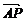 =(x-4,y),
=(x-4,y),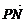 =(1-x,-y),
=(1-x,-y),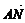 =(-3,0),∵
=(-3,0),∵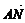 ·
·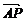 =6|
=6|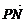 |,
|,
∴-3(x-4)=6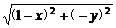 ,即3x2+4y2=12.
,即3x2+4y2=12.
∴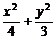 =1.∴P点的轨迹是以(-1,0)、(1,0)为焦点,长轴长为4的椭圆.
=1.∴P点的轨迹是以(-1,0)、(1,0)为焦点,长轴长为4的椭圆.
(2)N(1,0)为椭圆的右焦点,x=4为右准线,设P(x0,y0),P到右准线的距离为d,d=4-x0,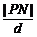 =e=
=e=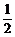 ,|PN|=
,|PN|=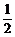 d=
d=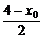 .∵-2≤x0≤2,∴1≤|PN|≤3.
.∵-2≤x0≤2,∴1≤|PN|≤3.
当|PN|=1时,P(2,0);当|PN|=3时,P(-2,0).
[探索题]已知向量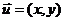 与
与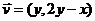 的对应关系用
的对应关系用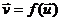 表示
表示
(1)
证明:对于任意向量 及常数m,n恒有
及常数m,n恒有
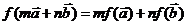 成立;
成立;
(2)
设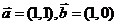 ,求向量
,求向量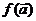 及
及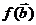 的坐标;
的坐标;
求使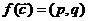 ,(p,q为常数)的向量
,(p,q为常数)的向量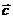 的坐标
的坐标
证:(1)设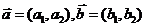 ,则
,则
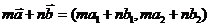 ,故
,故
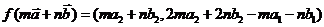
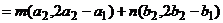 ,
,
∴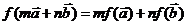
(2)由已知得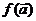 =(1,1),
=(1,1),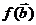 =(0,-1)
=(0,-1)
(3)设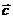 =(x,y),则
=(x,y),则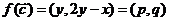 ,
,
∴y=p,x=2p-q,即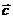 =(2P-q,p)
=(2P-q,p)
9.( 2005山东)已知向量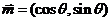 和
和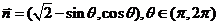 ,且
,且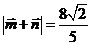 ,求
,求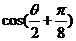 的值
的值
解: 因为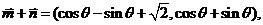
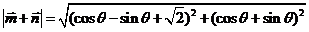
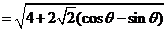
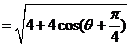
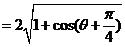
由已知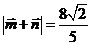 ,得
,得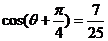

又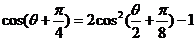
所以 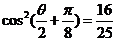

∵ 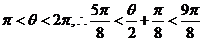 所以
所以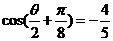
8.已知点A(2,3),B(5,4),C(7,10),若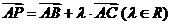 ,试问
,试问
(1)λ为何值时,点P在一、三象限角平分线上?
(2)λ为何值时,点P第三象限?
解.设点P的坐标为(x,y),则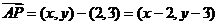
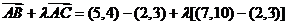
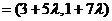 ,由
,由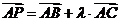 得
得
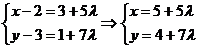 ,点P坐标为(5+5λ,4+7λ).
,点P坐标为(5+5λ,4+7λ).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com