
4.注意代换后参数的等价性
例8已知y=2sinθcosθ+sinθ-cosθ(0≤θ≤π),求y的最大值、最小值
解:设t=sinθ-cosθ=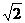 sin(θ-
sin(θ-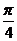 )
)
∴2sinθcosθ=1-t2
∴y=-t2+t+1=-(t-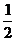 )2+
)2+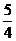
又∵t=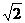 sin(θ-
sin(θ-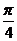 ),0≤θ≤π
),0≤θ≤π
∴-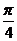 ≤θ-
≤θ-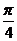 ≤
≤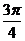
∴-1≤t≤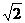
当t=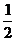 时,ymax=
时,ymax=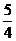
当t=-1时,ymin=-1
说明:此题在代换中,据θ范围,确定了参数t∈[-1,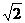 ],从而正确求解,若忽视这一点,会发生t=
],从而正确求解,若忽视这一点,会发生t=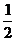 时有最大值而无最小值的结论
时有最大值而无最小值的结论
3.注意题中字母(参数)的讨论
例7求函数y=sin2x+acosx+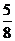 a-
a-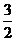 (0≤x≤
(0≤x≤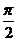 )的最大值
)的最大值
解:∵y=1-cos2x+acosx+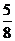 a-
a-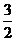 =-(cosx-
=-(cosx-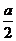 )2+
)2+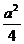 +
+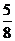 a-
a-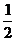
∴当0≤a≤2时,cosx=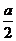 ,ymax=
,ymax=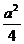 +
+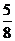 a-
a-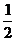
当a>2时,cosx=1,ymax=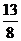 a-
a-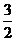
当a<0时,cosx=0,ymax=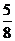 a-
a-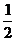
说明:解此题注意到参数a的变化情形,并就其变化讨论求解,否则认为cosx=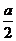 时,y有最大值会产生误解
时,y有最大值会产生误解
2.注意条件中角的范围
例6已知|x|≤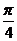 ,求函数y=cos2x+sinx的最小值
,求函数y=cos2x+sinx的最小值
解:y=-sin2x+sinx+1=-(sinx-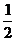 )2+
)2+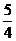
∵-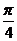 ≤x≤
≤x≤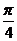
∴-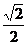 ≤sinx≤
≤sinx≤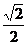
∴当sinx=-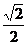 时
时
ymin=-(-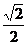 -
-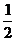 )2+
)2+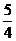 =
=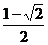
说明:解此题注意了条件|x|≤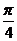 ,使本题正确求解,否则认为sinx=-1时y有最小值,产生误解
,使本题正确求解,否则认为sinx=-1时y有最小值,产生误解
三角函数最值问题是三角函数性质的重要内容之一,也是会考、高考必考内容,在求解中欲达到准确、迅速,除熟练掌握三角公式外,还应注意以下几点:
1.注意sinx、cosx自身的范围
例5求函数y=cos2x-3sinx的最大值
解:y=cos2x-3sinx=-sin2x-3sinx+1=-(sinx+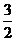 )2+
)2+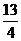
∵-1≤sinx≤1,
∴当sinx=-1时,ymax=3
说明:解此题易忽视sinx∈[-1,1]这一范围,认为sinx=-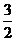 时,y有最大值
时,y有最大值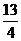 ,造成误解
,造成误解
利用变量代换,我们可把三角函数最值问题化成代数函数最值问题求解
例4求f(x)=sin4x+2sin3xcosx+sin2xcos2x+2sinxcos3x+cos4x的最大值和最小值
解:f(x)=(sin2x+cos2x)2-2sin2xcos2x+2sinxcosx(sin2x+cos2x)+sin2xcos2x=1+2sinxcosx-sin2xcos2x
令t=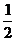 sin2x
sin2x
∴-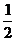 ≤t≤
≤t≤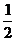 ①
①
f(t)=1+2t-t2=-(t-1)2+2 ②
在①的范围内求②的最值
当t=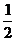 ,即x=kπ+
,即x=kπ+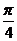 (k∈Z)时,f(x)max=
(k∈Z)时,f(x)max=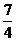
当t=-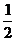 ,即x=kπ+
,即x=kπ+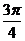 (k∈Z)时,f(x)min=-
(k∈Z)时,f(x)min=-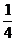
如果f(x)在[α,β]上是增函数,则f(x)在[α,β]上有最大值f(β),最小值f(α);如果f(x)在[α,β]上是减函数,则f(x)在[α,β]上有最大值f(α),最小值f(β)
例3 在0≤x≤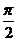 条件下,求y=cos2x-sinxcosx-3sin2x的最大值和最小值
条件下,求y=cos2x-sinxcosx-3sin2x的最大值和最小值
解:利用二倍角余弦公式的变形公式,有
y=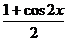 -2sin2x-3·
-2sin2x-3·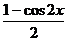 =2(cos2x-sin2x)-1
=2(cos2x-sin2x)-1
=2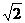 (cos2xcos
(cos2xcos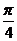 -sin2xsin
-sin2xsin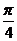 )-1
)-1
=2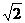 cos(2x+
cos(2x+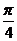 )-1
)-1
∵0≤x≤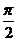 ,
,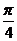 ≤2x+
≤2x+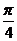 ≤
≤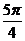
cos(2x+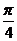 )在[0,
)在[0,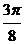 )上是减函数
)上是减函数
故当x=0时有最大值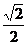
当x=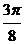 时有最小值-1
时有最小值-1
cos(2x+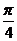 )在[
)在[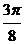 ,
,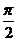 ]上是增函数
]上是增函数
故当x=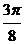 时,有最小值-1
时,有最小值-1
当x=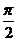 时,有最大值-
时,有最大值-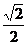
综上所述,当x=0时,ymax=1
当x=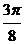 时,ymin=-2
时,ymin=-2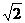 -1
-1
利用三角函数的有界性如|sinx|≤1,|cosx|≤1来求三角函数的最值
例2 a、b是不相等的正数
求y=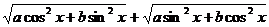 的最大值和最小值
的最大值和最小值
解:y是正值,故使y2达到最大(或最小)的x值也使y达到最大(或最小)
y2=acos2x+bsin2x+2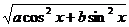 ·
·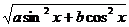 +asin2x+bcos2x
+asin2x+bcos2x
=a+b+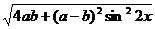
∵a≠b,(a-b)2>0,0≤sin22x≤1
∴当sin2x=±1时,即x=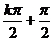 (k∈Z)时,y有最大值
(k∈Z)时,y有最大值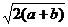 ;
;
当sinx=0时,即x=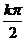 (k∈Z)时,y有最小值
(k∈Z)时,y有最小值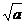 +
+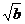

例1 求函数y=sin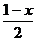 π的单调增区间
π的单调增区间
误解:令u=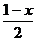 π
π
∵y=sinu在[2kπ-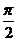 ,2kπ+
,2kπ+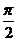 ](k∈Z)上递增
](k∈Z)上递增
∴2kπ-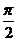 ≤
≤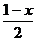 π≤2kπ+
π≤2kπ+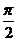
解得-4k≤x≤-4k+2
∴原函数的单调递增区间为[-4k,-4k+2](k∈Z)
分析:上述解答貌似正确,实则错误,错误的原因是,令u=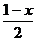 π,忽视了u是x的减函数,未考虑复合后单调性的变化
π,忽视了u是x的减函数,未考虑复合后单调性的变化
正解如下:
解法一:令u=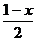 π,则u是x的减函数
π,则u是x的减函数
又∵y=sinu在[2kπ+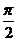 ,2kπ+
,2kπ+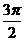 ](k∈Z)上为减函数,
](k∈Z)上为减函数,
∴原函数在[2kπ+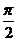 ,2kπ+
,2kπ+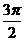 ](k∈Z)上递增
](k∈Z)上递增
设2kπ+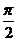 ≤
≤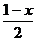 π≤2kπ+
π≤2kπ+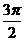
解得-4k-2≤x≤-4k(k∈Z)
∴原函数在[-4k-2,-4k](k∈Z)上单调递增
解法二:将原函数变形为y=-sin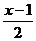 π
π
因此只需求sin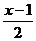 π=y的减区间即可
π=y的减区间即可
∵u=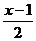 π为增函数
π为增函数
∴只需求sinu的递减区间
∴2kπ+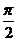 ≤
≤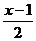 π≤2kπ+
π≤2kπ+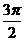
解之得:4k+2≤x≤4k+4(k∈Z)
∴原函数的单调递增区间为[4k+2,4k+4](k∈Z)
7.单调性
正弦函数在每一个闭区间[-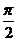 +2kπ,
+2kπ,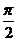 +2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[
+2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[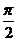 +2kπ,
+2kπ,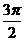 +2kπ](k∈Z)上都是减函数,其值从1减小到-1
+2kπ](k∈Z)上都是减函数,其值从1减小到-1
余弦函数在每一个闭区间[(2k-1)π,2kπ](k∈Z)上都是增函数,其值从-1增加到1;在每一个闭区间[2kπ,(2k+1)π](k∈Z)上都是减函数,其值从1减小到-1
6.奇偶性
y=sinx为奇函数,y=cosx为偶函数
正弦曲线关于原点O对称,余弦曲线关于y轴对称
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com