2．质量为m的汽车，启动后沿水平平直路面行驶，如果发动机的功率恒为P，且行驶过程中受到的摩擦阻力大小不变，汽车速度能够达到的最大值为V，那么当汽车的车速为v/4时，汽车的瞬时加速度的大小为 　　 (　 　　)

A．P/mv　 B．P/mv　 　C．3P/mv　 D．P/mv　　　

1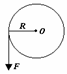．(南京一中08届高三第一次月考试卷)如图所示，某力F=10N作用于半径R=1m的转盘的边缘上，力F的大小保持不变，但方向始终保持与作用点的切线方向一致，则转动一周这个力F做的总功应为　　　　　 (　　　 )

A．0J　　 B．20πJ　 C．10J　 　D．20J

2．公式：(1)定义式_______，一般计算的是t时间内的　　　 　　功率。

　 (2)计算式　　　　　　 ， a为F与v的夹角。

　 若v是平均速度，则P为　　　　 ；

　 若v是瞬时速度，则P为　　　　 。

　 (3)单位：W，kW，l W=1J/s=1 N．m/s，

1 kW＝1×10³ W

思考题1：由P=W/t可以得出功的另一种计算方法W=Pt,因此"kW·h"是功的单位，它与“J”的换算关系如何？

思考题2： 额定功率与输出功率有什么区别？

知识点一合力功的计算计算方法

(1)合力做的功等于各力做功的代数和。

　 即W_合=W1+W2 +W3+…

　(2)先求出物体受到的合力F_合，再由W_合=F_合lcosa求解，但应注意a应为合力与位移l的夹角，F_合在运动过程中保持不变。

　 (3)利用动能定理：W_合=E_K2-E_K1。

[应用1]物体受到两个互相垂直的作用力F₁、F₂作用下从静止开始运动，已知力F₁做功6 J,则力F₁、F₂的合力对物体做功(　　 )

A．14 J 　　B．10 J 　　C．2 J　 　D．-2 J

导示:由于物体在两个相互垂直力作用下从静止开始运动，则两个力与位移的夹角都为锐角，两个力对物体都做正功，所以合力功大于任一分力功(即大于6 J)。

故选AB。

本题中用到功是标量，求合力功，算出各个力做的功，再代数和。

知识点二机车的两种启动方式

关于机车的启动问题的分析对机车来说，牵引力F和v共线，故有P=Fv。①当牵引力F一定时，P与速度v成正比(例：机车以恒定的加速度启动，P随v的增加而增大)；②当P一定时，速度v与牵引力F成反比(例：机车爬坡时，以减小v而获得较大的牵引力)。

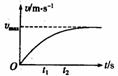　 (1)在额定功率P下启动：机车以恒定功率启动，若运动过程中所受阻力f不变，随着v的逐渐增大，牵引力逐渐减小，机车的加速度在逐渐减小。即机车启动后先做加速度逐渐减小的加速运动，再做匀

速运动．

其v-t图象如右图所示。

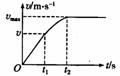(2)在恒定加速度a下启动：机车以恒定的加速度启动时．开始牵引力F=f+ma不变，当其速度增大到一定值时，其功率P达到最大值，下面的过程与上述(1)一样． 即机车启动后先做匀加速运动，后做加速度逐渐减小的加速运动，再做匀速运动．

其v-t图象如右图所示。

[应用2]汽车发动机的功率为60 kW,汽车的质量为4 t,当它行驶在坡度为0.02(sina=0.02)的长直公路上时,如图,所受阻力为车重的0.1倍(g＝10 m/s²),求：

(1)汽车所能达到的最大速度V_m=？

(2)若汽车从静止开始以0.6 m/s²的加速度做匀加速直线运动,则此过程能维持多长时间？

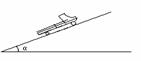(3)当汽车匀加速行驶的速度达到最大值时,汽车做功多少？

导示:(1)汽车在坡路上行驶,所受阻力由两部分构成,即f＝kmg+mgsinα=4000+800=4800 N.

所以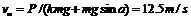

　(2)汽车从静止开始,以a=0.6 m/s²,匀加速行驶,有F′－f－mgsinα＝ma.

　所以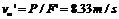

由运动学规律可以求出匀加速行驶的时间

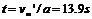
(3)由W=F·S可求出汽车在匀加速阶段行驶时做功为

W＝F·S＝4.16×10⁵J.

(1)注意匀加速结束时机车的速度并不是最后的最大速度．因此时F> f,之后还要在功率不变的情况下变加速一段时间才达到最后的最大速度v_max。

(2)P=Fv中的F是牵引力并非合力。

类型一平均功率与瞬时功率

[例1]在离地面5m高处以10 m/s的水平初速度抛出一个质量为1kg的物体，则(1)从抛出到落地全过程中重力的平均功率是多少？(2)物体落地时，重力的瞬时功率是多少？(不计空气阻力，g取10 m/s²)

导示:(1)物体从抛出到落地全过程中重力做功:W=mgh=1×10×5 J=50 J

下落时间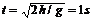

重力的平均功率：P=W/t=50 W

(2)物体落地时，竖直方向的瞬时速度

v＝gt＝10 m/s

重力的瞬时功率：P=mgv=1×10×10W=100W

　 　求功率时一定要分清是求哪个力的功率，还要分清是求平均功率还是瞬时功率。某一过程的功率指平均功率，某一时刻的功率指瞬时功率。

类型二变力功的计算

[例2]人在A点拉着绳通过一定滑轮吊起质量m=50 kg的物体，如图所示，开始时绳与水平方向夹角为60⁰，当人匀速提起重物由A点沿水平方向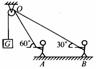运动s=2m而到达B点时，绳与水平方向成30⁰角，求人对绳的拉力做了多少功。

导示:人对绳的拉力方向时刻变化，力是变力因此不能利用W=Flcos a直接求拉力的功，但人对绳的拉力的功与绳对物体的拉力的功是相

等的，而绳对物体的拉力是恒力。

设滑轮距人手的高度为h，

则h(cot 30⁰-cot 60⁰)=s　　　　 ①

重物G上升的高度Δh=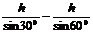

人对绳子做的功为W=mgΔh　　 ③

由①②③式代入数据可得：W=732J

思考题：若人由A以速度v匀速运动至B，人对绳做的功又是多大？

　变力的功

　 (l)用动能定理或功能关系求解

　 (2)将变力的功转化为恒力的功求解

　 ①当力的大小不变，而方向始终与运动方向相同或相反 时，这类力的功等于力和路程(不是位移)的乘积，如滑动 摩擦力、空气阻力做功，等等。

　 ②当力的方向不变，大小随位移做线性变化时，可先求出平均作用力，再由W=Flcos a计算，如弹簧弹力做功。

　 ③作出变力F随位移变化的图象，图线与横轴所夹的“面积”即为变力所做的功。

　 ④当变力的功率P一定时，可作W = Pt求功．如机车牵引力做的功。

类型三实际应用题

[例3]人的心脏每跳一次大约输送8×10^-5m³的血液，正常人血压(可看作心脏压送血液的压强)的平均值约为1.5×10⁴Pa，心跳约每分钟70次，据此估测心脏工作的平均功率。

导示:功的公式：W=FL

压强公式：P＇=F/S

所以心脏每跳一次做功：W=P＇SL

平均功率：P＝NW／t＝1.4W

1．定义：功跟完成这些功所用时间的比值叫功率。

功率是表征______________的物理量。

4．功是___________，即功必定对应某一位移(过程)。

3．功是_____量，只有大小，没有方向，但有正负。

　 (1)当0⁰<a<90⁰时，W>0，力对物体做____功。

　 (2)当90⁰<a<180⁰时，W<0，力对物体做____功。也称物体克服这个力做了功。

　 (3)当a=90⁰时，W=0，力对物体__________。

思考题：“正功”和“负功”的物理意义是什么？

2．公式：_____________。适用于恒力做功(a代表力的方向和位移方向的夹角)。

两种理解：一种是力“F”乘以物体在力的方向上发生的位移“lcos a”；另一种是在位移“l”方向上的力“Fcos a”乘以位移l。

1．做功的两个要素：_______和________________。

12．(14分)(2010·合肥联考)已知两个命题r(x)：sin x+cos x>m，s(x)：x²+mx+1>0.如果对

∀x∈R，r(x)与s(x)有且仅有一个是真命题，求实数m的取值范围．

解　∵sin x+cos x＝sin≥－，

∴当r(x)是真命题时，m<－.

又∵对∀x∈R，s(x)为真命题，即x²+mx+1>0恒成立，有Δ＝m²－4<0，∴－2<m<2.

∴当r(x)为真，s(x)为假时，m<－，

同时m≤－2或m≥2，即m≤－2，

当r(x)为假，s(x)为真时，m≥－且－2<m<2，

即－≤m<2.

综上所述，m的取值范围是m≤－2或－≤m<2.

11．(13分)(2010·常德调研)写出由下列各组命题构成的“p或q”，“p且q”，“非p”形

式的新命题，并判断其真假．

(1)p：2是4的约数，q：2是6的约数；

(2)p：矩形的对角线相等，q：矩形的对角线互相平分；

(3)p：方程x²+x－1＝0的两实根的符号相同，q：方程x²+x－1＝0的两实根的绝对值相

等．

解　(1)p或q：2是4的约数或2是6的约数，真命题；

p且q：2是4的约数且2也是6的约数，真命题；

非p：2不是4的约数，假命题．

(2)p或q：矩形的对角线相等或互相平分，真命题；

p且q：矩形的对角线相等且互相平分，真命题；

非p：矩形的对角线不相等，假命题．

(3)p或q：方程x²+x－1＝0的两个实数根符号相同或绝对值相等，假命题；

p且q：方程x²+x－1＝0的两个实数根符号相同且绝对值相等，假命题；

非p：方程x²+x－1＝0的两实数根符号不同，真命题．