
5.在相同的 和 下,相同体积的任何 都含有 的粒子。
[讨论]下列有关气体的叙述中,错误的是( )
A. 不同的气体,若体积不同,则它们所含的分子数肯定不同
B.当分子数目相同时,气体体积的大小主要决定于气体分子之间的距离
C. 一定温度和压强下,气体分子的物质的量决定了它们的体积
D. 在标准状况下,的混合物
[课堂练习](1)标准状况下:22g CO2的体积是 ,其中所含分子数与 gO2相同。
(2)0.01 mol某气体的质量是0.28g,该气体的摩尔质量是 ;在标准状况下,
该气体的密度是 。
(3)相同条件下,CH4与O2的质量比是1:8时二者的体积比是 。
4.物质体积的大小取决于构成这种物质的 、 和
这三个因素。 叫气体摩尔体积,用符号 表示,常用的单位有 (或)和 。通常将 ℃、 Pa时的状况称为标准状况。标准状况下的气体摩尔体积为 。
中所含的碳原子总数为A
3.1mol任何粒子集合体都含有 个粒子;而任何粒子或物质的质量在以 为单位时,其数值都与该粒子的 或 相等。将 叫做摩尔质量。摩尔质量的符号为 ,单位常用 或 。
物质的量(n)、物质的质量(m)、摩尔质量(M)三者之间的关系式是: n=
2.1mol任何粒子集体所含的粒子数与0.012kg 中所含的原子数相等,约
为 ,把 叫做 常数,并作为一个 ,符号为 。物质的量只适用于微观粒子,使用摩尔作单位时,必须指明粒子的种类并且要用化学式来表示。
[讨论]下列说明是否正确?为什么?
(1)0.5mol氧气 ;
(2)0.2mol氢分子 ;
(3)0.3mol钠离子 ;(4)10mol氮 ;
(5)4 mol苹果 。
1.1971年,在第十四届国际计量大会上决定用 作为计量原子、分子或离子等微观粒子的“物质的量”的单位。“物质的量”的符号为 ,实际上表示含有一定数目 的集合体。
20.(本小题满分14分)
已知点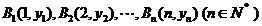 在直线
在直线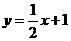 上,点
上,点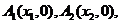
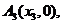 ……,
……,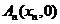 顺次为
顺次为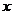 轴上的点,其中
轴上的点,其中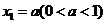 ,对于任意
,对于任意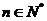 ,点
,点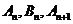 构成以
构成以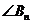 为顶角的等腰三角形, 设
为顶角的等腰三角形, 设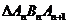 的面积为
的面积为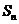 .
.
(1)证明:数列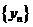 是等差数列;
是等差数列;
(2)求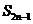 (用
(用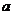 和
和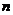 的代数式表示);
的代数式表示);
(3)设数列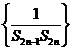 前
前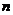 项和为
项和为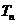 ,判断
,判断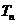 与
与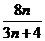 (
(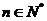 )的大小,并证明你的结论;
)的大小,并证明你的结论;
解:(1)由于点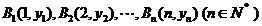 在直线
在直线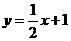 上,
上,
则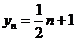 ,
,
因此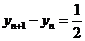 ,所以数列
,所以数列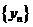 是等差数列
是等差数列
(2)由已知有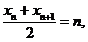 ,那么
,那么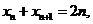 同理
同理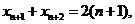
以上两式相减,得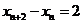 ,
,
∴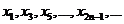 成等差数列;
成等差数列;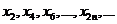 也成等差数列,
也成等差数列,
∴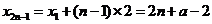 ,
,
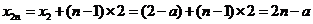
点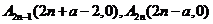 ,则
,则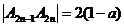 ,
,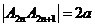 ,
,
而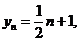
∴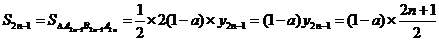
(3)由(1)得: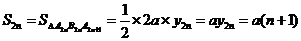 ,
,
则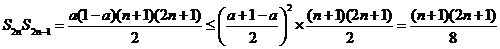
而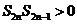 ,则
,则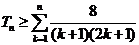 ,
,
即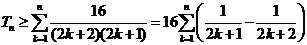
∴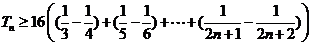
∴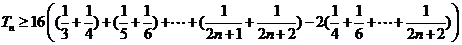
∴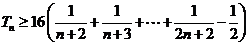
由于 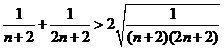 ,
,
而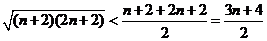 ,
,
则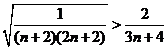 , 从而
, 从而 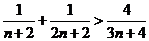 ,
,
同理: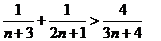
……
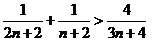
以上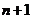 个不等式相加得:
个不等式相加得: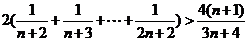
即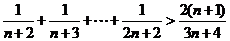 ,
,
从而 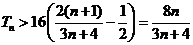 。
。
19.(本小题满分14分)
已知数列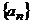 中,
中,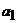 =1,
=1, 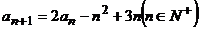 ,
,
(1)是否存在常数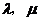 ,使得数列
,使得数列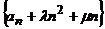 是等比数列,若存在,求
是等比数列,若存在,求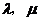 的值,若不存在,说明理由。
的值,若不存在,说明理由。
(2)设 ,数列
,数列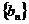 的前n项和为
的前n项和为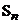 ,是否存在常数c,使得
,是否存在常数c,使得

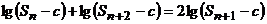 成立?并证明你的结论。
成立?并证明你的结论。
(3)设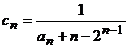 ,
,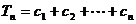 ,证明
,证明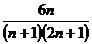 <
<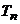 <
<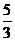
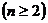 。
。
解:(1)设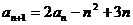 可化为
可化为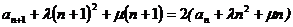 ,
,
即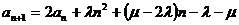 ,故
,故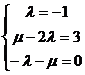 ,得
,得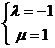 。
。
又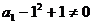 ,所以存在
,所以存在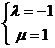 ,使得数列
,使得数列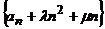 是等比数列。
是等比数列。
(2)由(1)得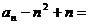
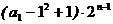 ,得
,得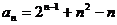 ,所以
,所以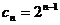 。
。
要使得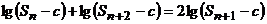 成立,
成立,
则有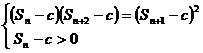 ,得
,得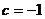 。所以,存在常数
。所以,存在常数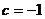 ,使得
,使得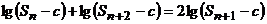 成立。
成立。
(3)证明:因为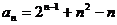 ,所以
,所以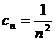 ,而
,而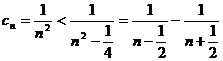 ,
,
所以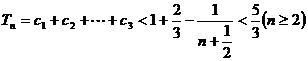 。
。
又当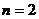 时,
时,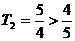 ,符合。
,符合。
当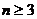 时,
时,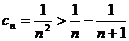 ,
,
得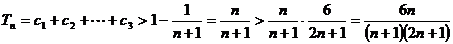 。
。
综上,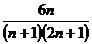 <
<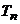 <
<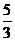
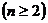 得证。
得证。
18.(本小题满分14分)
关于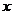 的不等式
的不等式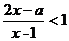 的解集为P, 不等式
的解集为P, 不等式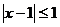 的解集为Q,若P
的解集为Q,若P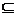 Q,,求实数
Q,,求实数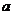 的取值范围。
的取值范围。
解:Q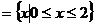 , 对于
, 对于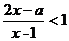 ,当
,当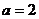 时,P=
时,P=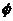 ,符合。
,符合。
当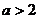 时,P
时,P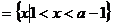 ,此时只需
,此时只需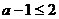 ,即
,即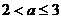 。
。
当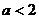 时,P
时,P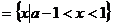 ,此时只需
,此时只需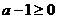 ,即
,即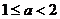 。
。
综上,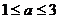 为所求。
为所求。
17.(本小题满分14分)
为保增长、促发展,某地计划投资甲、乙两项目,市场调研得知,甲项目每投资100万元需要配套电能2万千瓦,可提供就业岗位24个,增加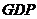 260万元;乙项目每投资100万元需要配套电能4万千瓦,可提供就业岗位32个,增加
260万元;乙项目每投资100万元需要配套电能4万千瓦,可提供就业岗位32个,增加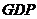 200万元.已知该地为甲、乙两项目最多可投资3000万元,配套电能100万千瓦,并要求它们提供的就业岗位不少于800个.如何安排甲、乙两项目的投资额,增加的
200万元.已知该地为甲、乙两项目最多可投资3000万元,配套电能100万千瓦,并要求它们提供的就业岗位不少于800个.如何安排甲、乙两项目的投资额,增加的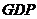 最大?
最大?
解:设甲项目投资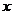 (单位:百万元),乙项目投资
(单位:百万元),乙项目投资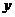 (单位:百万元),两项目增加的
(单位:百万元),两项目增加的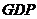 为
为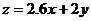 。
。
 依题意,
依题意,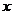 、
、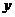 满足
满足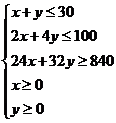 ,所确定的平面区域如图中阴影部分
,所确定的平面区域如图中阴影部分
解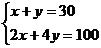 得
得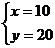 ,
,
解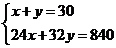 得
得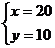
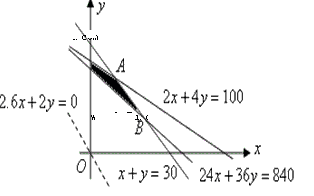
设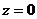 ,得
,得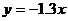 ,将直线
,将直线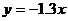 平移至经过点
平移至经过点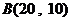 ,
,
即甲项目投资2000万元,、乙项目投资1000万元,两项目增加的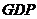 最大
最大
16.(本小题满分12分)
已知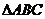 中,
中,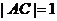 ,
,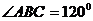 ,
,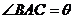 ,记
,记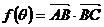 ,
,
(1)求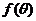 关于
关于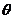 的表达式;
的表达式;
(2)求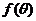 的值域;
的值域;
解:(1)由正弦定理有: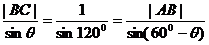 ;
;
∴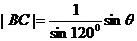 ,
,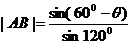 ;
;
∴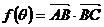
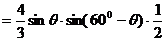
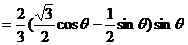
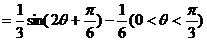
(2)由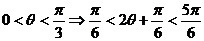 ;
;
∴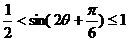 ;∴
;∴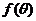
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com