
1.如果直线y=3x+6与y=2x-4交点坐标为(a,b),则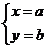 是方程组_______的解(
)
是方程组_______的解(
)
A.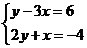 B.
B.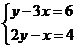 C.
C.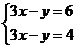 D.
D.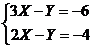
2.灵活运用函数知识解决实际问题.
学习难点
灵活运用函数知识解决相关实际问题.
预习问题
我们知道,方程3x+5y=8可以转化为y=-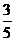 x+
x+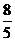 ,并且直线y=-
,并且直线y=-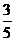 x+
x+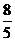 上每个点的坐标(x,y)都是方程3x+5y=8的解.
上每个点的坐标(x,y)都是方程3x+5y=8的解.
由于任何一个二元一次方程都可以转化为y=kx+b的形式.所以每个二元一次方程都对应一个一次函数,也就是对应一条直线.
那么解二元一次方程组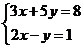
可否看作求两个一次函数y=-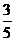 x+
x+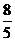 与y=2x-1图象的交点坐标呢?如果可以,我们是否可以用画图象的方法来解二元一次方程组呢?
与y=2x-1图象的交点坐标呢?如果可以,我们是否可以用画图象的方法来解二元一次方程组呢?
预习一下,看能否解决这些问题.
魔法师
例:在直角坐标系中有两条直线:L1:y=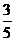 x+
x+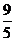 和L2:y=-
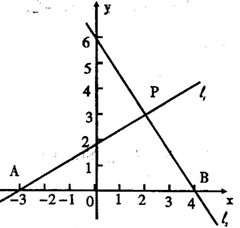
和L2:y=-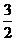 x+6,它们的交点为P,第一条直线L与x轴交于点A,第二条直线L与x轴交于点B.(1)A、B两点的坐标;(2)用图象法解方程组:
x+6,它们的交点为P,第一条直线L与x轴交于点A,第二条直线L与x轴交于点B.(1)A、B两点的坐标;(2)用图象法解方程组: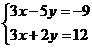 ;(3)求△PAB的面积.
;(3)求△PAB的面积.
分析:(1)由“直线上点的坐标与二元一次方程的解的关系”以及“直线与x轴的交点的纵坐标为0”确定A、B两点的坐标.
(2)方程组中的两个方程变形后正好是该题中的两个函数,交点P(2,3)的坐标即方程组的解.
(3)AB=7,AB边上的高是P点纵坐标的绝对值,从而求出面积.
解:(1)由y=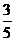 x+
x+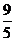 ,当y=0时,x=-3, ∴A(-3,0)
,当y=0时,x=-3, ∴A(-3,0)
由y=-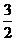 x+6,当y=0时,x=4, ∴B(4,0)
x+6,当y=0时,x=4, ∴B(4,0)
(2)由3x-5y=-9,可得y=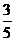 x+
x+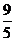
同理,由3x+2y=12,可得y=-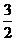 x+6
x+6
在同一直角坐标系内作出一次函数y=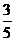 x+
x+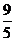 的图象和y=-
的图象和y=-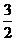 x+6的图象,
x+6的图象,
观察图象(如图),得L1、L2的交点为P(2,3)
∴方程组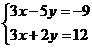 的解是
的解是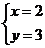
(3)S△ABP=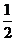 ×(OA+OB)×3=10.5
×(OA+OB)×3=10.5
演兵场
☆我能选
1.归纳图象法解二元一次方程组的具体方法.
2.两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.
学习重点
1.解关于x、y的方程组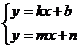 ,从“数”的角度看,相当于考虑当自变量为何值时两个函数的值相等,以及这个函数值是多少,从“形”的角度看,相当于确定两条直线y=kx+b与y=mx+n的交点坐标.
,从“数”的角度看,相当于考虑当自变量为何值时两个函数的值相等,以及这个函数值是多少,从“形”的角度看,相当于确定两条直线y=kx+b与y=mx+n的交点坐标.
11.3.3 一次函数与二元一次方程(组)
学习目标
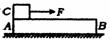
5.如图所示,长 L=1m,质量 M=1kg的木板AB静止在光滑的水平面上,在木板的最左端A处有一个质量m=1kg的小物体C静止在木板上,现用F=20N的水平恒力作用于物体C上,使它由静止开始向右运动.已知C与木板间滑动摩擦因数μ=0.5,g=10m/s2,求物体 C由 A端运动到 B端时,水平恒力对物体C所做的功?
答案:1.B 2.C 3.AB 4.1000J 5.30J
4.一人从10 m深的井中,用一质量为1kg的桶盛10 kg的水匀速向上提(绳子的重力不计),由于水桶不断漏水,每升高lm漏掉0.2 kg的水,则把这桶水提上来需做多少功?
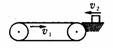
3.(常州第一中学08届第2次月考)如图所示,一水平方向足够长的传送带以恒定的速度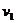 沿顺时针方向运动,传送带右端有一与传送带等高的光滑水平面,物体以速率
沿顺时针方向运动,传送带右端有一与传送带等高的光滑水平面,物体以速率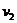 沿直线向左滑上传送带后,经过一段时间又返回光滑水平面上,这时速率为
沿直线向左滑上传送带后,经过一段时间又返回光滑水平面上,这时速率为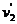 ,则下列说法正确的是 ( )
,则下列说法正确的是 ( )
 A.若
A.若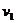 <
<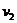 ,则
,则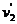 =
= 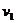
B.若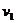 >
>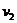 ,则
,则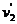 =
= 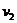
C.不管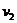 多大,总有
多大,总有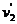 =
= 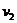
D.只有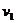 =
= 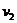 时,才有
时,才有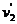 =
=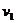
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com