5．解综合题的成败在于审清题目，弄懂来龙去脉，透过给定信息的表象，抓住问题的本质，揭示问题的内在联系和隐含条件，明确解题方向，形成解题策略．

4．数列极限的综合题形式多样，解题思路灵活，但万变不离其宗，就是离不开数列极限的概念和性质，离不开数学思想方法，只要能把握这两方面，就会迅速打通解题思路．

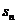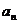3．注意与之间关系的转化。如：

=　 ，　 =．

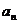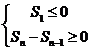
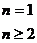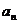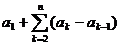2．在解决等差数列或等比数列的相关问题时，“基本量法”是常用的方法，但有时灵活地运用性质，可使运算简便，而一般数列的问题常转化为等差、等比数列求解。

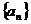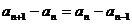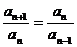1．证明数列是等差或等比数列常用定义，即通过证明 或而得。

3.数列求和的常用方法：公式法、裂项相消法、错位相减法、倒序相加法等。

2. 在等差数列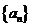中,有关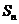的最值问题--常用邻项变号法求解：　

(1)当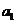>0,d<0时，满足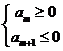的项数m使得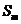取最大值.

(2)当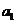<0,d>0时，满足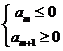的项数m使得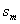取最小值。

在解含绝对值的数列最值问题时,注意转化思想的应用。

1．判断和证明数列是等差(等比)数列常有三种方法：

(1)定义法：对于n≥2的任意自然数,验证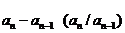为同一常数。

(2)通项公式法：

①若　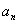 =　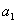+(n-1)d=　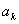+(n-k)d ，则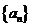为等差数列；

②若　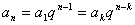 ，则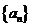为等比数列。

(3)中项公式法：验证中项公式成立。

3．培养学生善于分析题意，富于联想，以适应新的背景，新的设问方式，提高学生用函数的思想、方程的思想研究数列问题的自觉性、培养学生主动探索的精神和科学理性的思维方法．