
5、(浙江卷)
15.[答案]: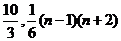
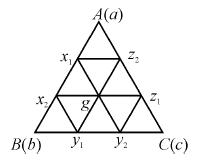
[解析]当n=3时,如图所示分别设各顶点的数用小写字母表示,即由条件知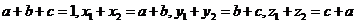
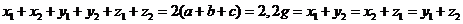
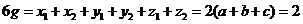
即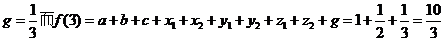
进一步可求得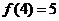 。由上知
。由上知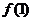 中有三个数,
中有三个数,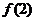 中 有6个数,
中 有6个数,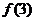 中共有10个数相加 ,
中共有10个数相加 ,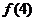 中有15个数相加….,若
中有15个数相加….,若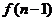 中有
中有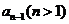 个数相加,可得
个数相加,可得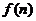 中有
中有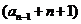 个数相加,且由
个数相加,且由
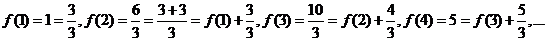
可得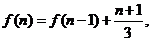 所以
所以
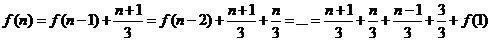
=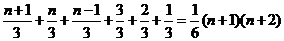
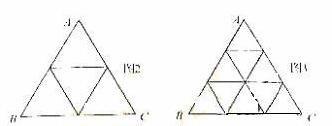
4、(湖南卷) 15、将正⊿ABC分割成
 (
(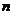 ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)=
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= 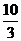 ,…,f(n)=
,…,f(n)= 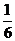 (n+1)(n+2)
(n+1)(n+2)
3、(北京卷理)14.已知数列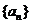 满足:
满足: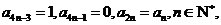 则
则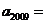 ________;
________;
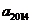 =_________.
=_________.
[答案]1,0
[解析]本题主要考查周期数列等基础知识.属于创新题型.
依题意,得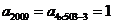 ,
,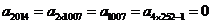 .
.
∴应填1,0.
2、(江苏卷)8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为 ▲ .

[解析] 考查类比的方法。体积比为1:8 
10.[答案]C
[解析][解析]由图形可得三角形数构成的数列通项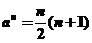 ,同理可得正方形数构成的数列通项
,同理可得正方形数构成的数列通项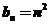 ,则由
,则由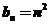
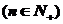 可排除A、D,又由
可排除A、D,又由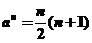 知
知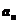 必为奇数,故选C.
必为奇数,故选C.
1、(湖北卷理) 10.古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如: 

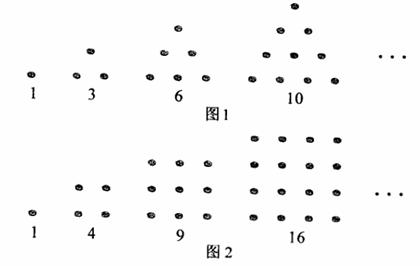
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数。下列数中既是三角形数又是正方形数的是
A.289 B.1024 C.1225 D.1378
19、(北京卷理)6.若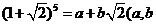 为有理数),则
为有理数),则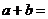

 ( )
( )
A.45 B.55 C.70 D.80
[答案]C
[解析]本题主要考查二项式定理及其展开式. 属于基础知识、基本运算的考查.
∵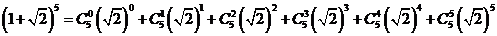
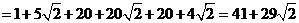 ,
, 

由已知,得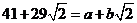 ,∴
,∴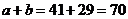 .故选C.
.故选C.
18、(重庆卷)3.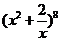 的展开式中
的展开式中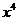 的系数是( D
)
的系数是( D
)
A.16 B.70 C.560 D.1120
17、(浙江卷) 4.在二项式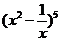 的展开式中,含
的展开式中,含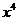 的项的系数是( )
的项的系数是( )


A.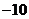 B.
B.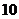
C.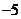 D.
D.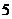
答案:B
[解析]对于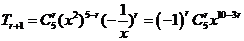 ,对于
,对于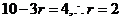 ,则
,则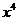 的项的系数是
的项的系数是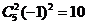
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com