
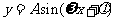 为奇函数
为奇函数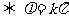 ;函数
;函数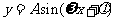 为偶函数
为偶函数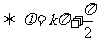
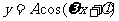 为偶函数
为偶函数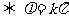 ;函数
;函数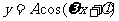 为奇函数
为奇函数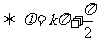
 函数
函数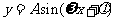
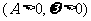 的单调增区间可由
的单调增区间可由
解出,单调减区间可由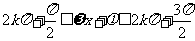 解出;
解出;
函数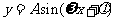
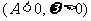 的单调增区间可由
的单调增区间可由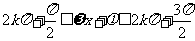
解出,单调减区间可由
 解出
解出
三角函数的奇偶性和单调性具体如下表:
|
函数 |
奇偶性 |
单调区间 |
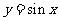 |
奇 |
在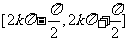 上增 上增在 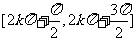 减 减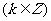 |
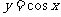 |
偶 |
在 上增 上增在 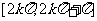 减 减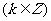 |
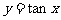 |
奇 |
在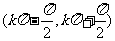 上增 上增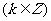 |
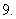 (
(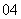 四川)函数
四川)函数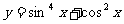 的最小正周期为
的最小正周期为 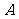
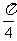
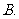
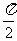
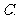
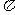
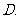
 (
( 上海)函数
上海)函数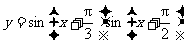 的最小正周期
的最小正周期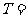
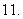 (
(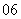 福建)已知函数
福建)已知函数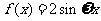
 在区间
在区间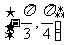 上的最小值是
上的最小值是 ,则
,则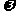
的最小值等于 
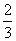
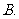
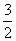
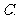
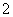
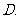
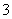
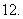 (
(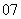 安徽文)解不等式
安徽文)解不等式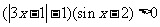 .
.
 (
( 天津)已知函数
天津)已知函数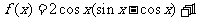 ,
,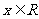 .
.
(Ⅰ)求函数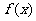 的最小正周期;
的最小正周期;
(Ⅱ)求函数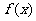 在区间
在区间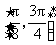 上的最小值和最大值.
上的最小值和最大值.
 (
( 重庆)设
重庆)设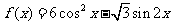 .(Ⅰ)求
.(Ⅰ)求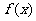 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)若锐角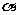 满足
满足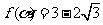 ,求
,求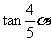 的值.
的值.
 求函数
求函数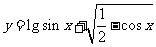 的定义域.
的定义域.
 函数
函数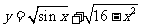 的定义域为
的定义域为
 若方程
若方程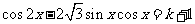 有解,则
有解,则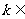
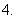 (
(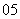 江西)设函数
江西)设函数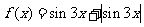 ,则
,则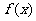 为
为
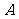 周期函数,最小正周期为
周期函数,最小正周期为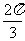
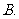 周期函数,最小正周期为
周期函数,最小正周期为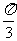
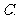 周期函数,数小正周期为
周期函数,数小正周期为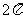
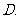 非周期函数
非周期函数
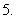 (
(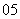 全国Ⅱ)函数
全国Ⅱ)函数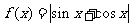 的最小正周期是
的最小正周期是 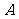
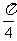
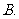
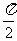
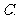
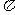
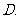 2
2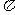
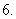 函数
函数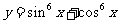 的最小正周期为
的最小正周期为
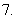 函数
函数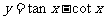 的周期是
的周期是
 已知函数
已知函数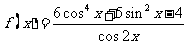 ,求
,求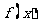 的定义域,判断它的奇偶性,并求其值域
的定义域,判断它的奇偶性,并求其值域
问题1. 求下列函数的定义域:
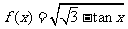 ;
;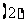
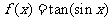 ;
;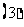
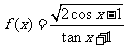
问题2.求下列函数的值域:
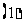
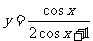 ;
;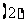
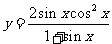 ;
;
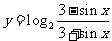 ;
;
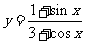 .
.
问题3.求下列函数的周期:
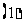
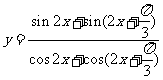 ;
;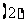
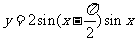 ;
;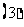
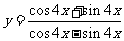
问题4.已知函数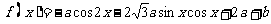 的定义域为
的定义域为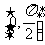 ,值域为
,值域为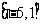 ,求常数
,求常数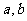 的值.
的值.
 求三角函数的定义域实质就是解三角不等式(组).一般可用三角函数的图象或三角函数线确定三角不等式的解.列三角不等式,既要考虑分式的分母不能为零;偶次方根被开方数大于等于零;对数的真数大于零及底数大于零且不等于1,又要考虑三角函数本身的定义域;
求三角函数的定义域实质就是解三角不等式(组).一般可用三角函数的图象或三角函数线确定三角不等式的解.列三角不等式,既要考虑分式的分母不能为零;偶次方根被开方数大于等于零;对数的真数大于零及底数大于零且不等于1,又要考虑三角函数本身的定义域;
 求三角函数的值域的常用方法:①化为求代数函数的值域;②化为求
求三角函数的值域的常用方法:①化为求代数函数的值域;②化为求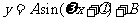 的值域;③化为关于
的值域;③化为关于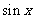 (或
(或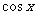 )的二次函数式;
)的二次函数式;
 三角函数的周期问题一般将函数式化为
三角函数的周期问题一般将函数式化为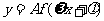 (其中
(其中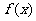 为三角函数,
为三角函数, ).
).
三角函数的定义域、值域及周期如下表:
|
函数 |
定义域 |
值域 |
周期 |
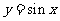 |
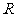 |
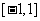 |
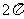 |
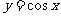 |
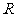 |
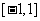 |
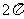 |
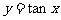 |
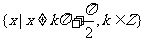 |
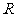 |
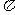 |
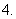 (
( 天津)要得到函数
天津)要得到函数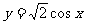 的图象,只需将函数
的图象,只需将函数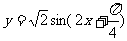 的
的
图象上所有的点的
 横坐标缩短到原来的
横坐标缩短到原来的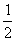 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动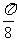 个单位长度
个单位长度
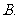 横坐标缩短到原来的
横坐标缩短到原来的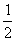 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动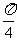 个单位长度
个单位长度
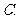 横坐标伸长到原来的
横坐标伸长到原来的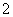 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动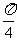 个单位长度
个单位长度
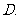 横坐标伸长到原来的
横坐标伸长到原来的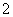 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动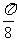 个单位长度
个单位长度
 (
( 江苏)为了得到函数
江苏)为了得到函数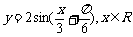 的图像,只需把函数
的图像,只需把函数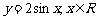 的图像上所有的点
的图像上所有的点
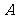 向左平移
向左平移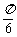 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的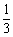 倍(纵坐标不变)
倍(纵坐标不变)
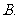 向右平移
向右平移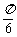 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的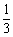 倍(纵坐标不变)
倍(纵坐标不变)
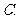 向左平移
向左平移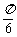 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的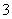 倍(纵坐标不变)
倍(纵坐标不变)
 向右平移
向右平移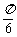 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的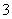 倍(纵坐标不变)
倍(纵坐标不变)
 (
( 安徽)函数
安徽)函数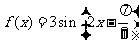 的图象为
的图象为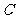 ,
,
①图象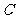 关于直线
关于直线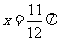 对称;②函数
对称;②函数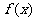 在区间
在区间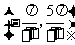 内是增函数;
内是增函数;
③由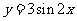 的图象向右平移
的图象向右平移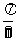 个单位长度可以得到图象
个单位长度可以得到图象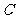 .
.
以上三个论断中,正确论断的个数是 
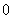
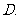
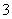
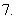
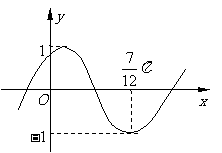 (
( 安徽)将函数
安徽)将函数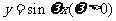 的图象按向量
的图象按向量
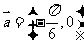 平移,平移后的图象如图所示,
平移,平移后的图象如图所示,
则平移后的图象所对应函数的解析式是
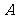
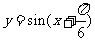
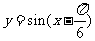
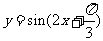
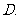
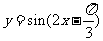
 (
( 福建)函数
福建)函数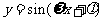
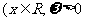 ,
,
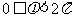 )的部分图象如图,则
)的部分图象如图,则
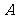
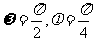
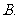
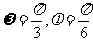
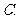
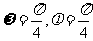
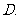
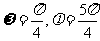
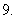 (
( 福建)已知函数
福建)已知函数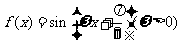 的最小正周期为
的最小正周期为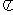 ,则该函数的图象
,则该函数的图象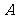 关于点
关于点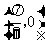 对称
对称 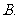 关于直线
关于直线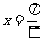 对称
对称
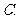 关于点
关于点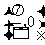 对称
对称 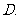 关于直线
关于直线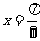 对称
对称
 (
( 广东文)已知简谐运动
广东文)已知简谐运动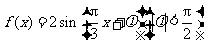 的图象经过点
的图象经过点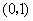 ,则该简谐运动的最小正周期
,则该简谐运动的最小正周期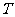 和初相
和初相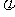 分别为
分别为
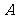
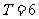 ,
,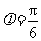 ;
;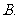
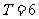 ,
,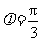 ;
;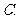
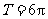 ,
,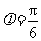 ;
;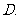
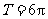 ,
,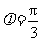
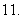 (
( 陕西)已知函数
陕西)已知函数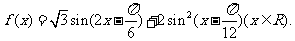
(Ⅰ)求函数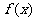 的最小正周期;(Ⅱ)求使函数
的最小正周期;(Ⅱ)求使函数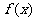 取得最大值的
取得最大值的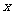 集合.
集合.
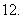 (
(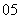 全国Ⅰ文)设函数
全国Ⅰ文)设函数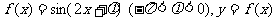 图像的一条对称轴是直线
图像的一条对称轴是直线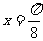 .(Ⅰ)求
.(Ⅰ)求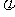 ;(Ⅱ)求函数
;(Ⅱ)求函数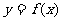 的单调增区间;
的单调增区间;
(Ⅲ)画出函数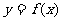 在区间
在区间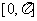 上的图像。
上的图像。
 (
( 全国)已知函数
全国)已知函数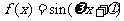
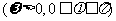 是
是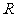 上的偶函数,其图象关于点
上的偶函数,其图象关于点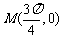 对称,且在区间
对称,且在区间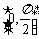 上是单调函数。求
上是单调函数。求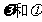 的值。
的值。
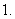 要得到
要得到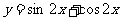 的图象,只需将
的图象,只需将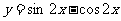 的图象
的图象
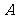 向左平移
向左平移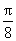
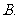 向右平移
向右平移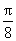
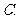 向左平移
向左平移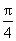
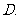 向右平移
向右平移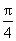
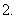 如果函数
如果函数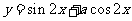 的图象关于直线
的图象关于直线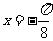 对称,则
对称,则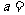
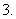 函数
函数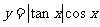 的部分图象是
的部分图象是
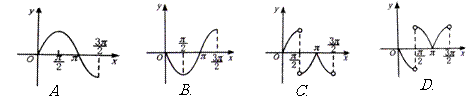
问题1. 已知函数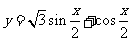
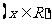 .
.
 用“五点法”画出它的图象;
用“五点法”画出它的图象; 求它的振幅、周期和初相;
求它的振幅、周期和初相;
 说明该函数的图象可由
说明该函数的图象可由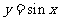 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
问题2.
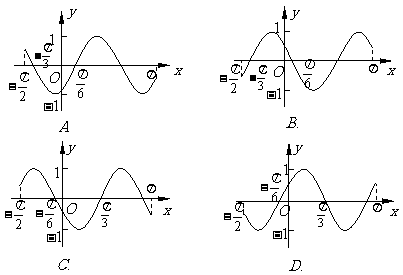 (
( 海南)函数
海南)函数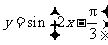 在区
在区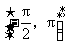 的简图是
的简图是
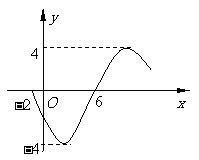 (
( 天津文)函数
天津文)函数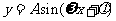
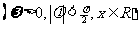
的部分图象如图所示,则函数表达式为
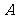
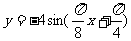
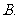
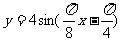
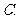
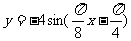
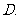
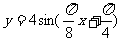
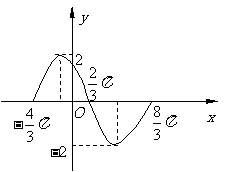
 已知函数
已知函数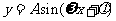 (
(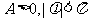 )
)
的一段图象如下图所示,求该函数的解析式.
问题3. 将函数
将函数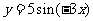 的周期扩大到原来的
的周期扩大到原来的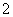 倍,再将函数图象左移
倍,再将函数图象左移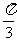 ,得到图象对应解析式是
,得到图象对应解析式是
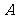
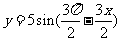
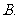
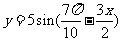
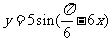
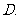
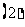 (
( 山东文)要得到函数
山东文)要得到函数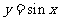 的图象,只需将函数
的图象,只需将函数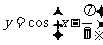
的图象 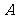 向右平移
向右平移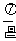 个单位;
个单位;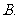 向右平移
向右平移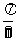 个单位;
个单位;
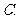 向左平移
向左平移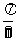 个单位;
个单位;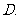 向左平移
向左平移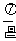 个单位
个单位
 (
( 山东)为了得到函数
山东)为了得到函数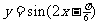 的图象,可以将函数
的图象,可以将函数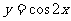 的图象
的图象
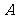 向右平移
向右平移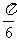 个单位长度
个单位长度
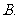 向右平移
向右平移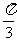 个单位长度
个单位长度
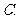 向左平移
向左平移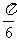 个单位长度
个单位长度 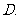 向左平移
向左平移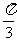 个单位长度
个单位长度
问题4. (
( 福建)已知函数
福建)已知函数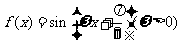 的最小正周期为
的最小正周期为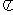 ,则
,则
该函数的图象 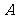 关于点
关于点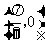 对称
对称 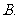 关于直线
关于直线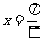 对称
对称
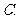 关于点
关于点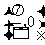 对称
对称 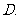 .关于直线
.关于直线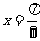 对称
对称
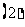 (
( 山东)已知函数
山东)已知函数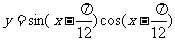 ,则下列判断正确的是
,则下列判断正确的是
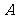 此函数的最小正周期为
此函数的最小正周期为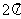 ,其图象的一个对称中心是
,其图象的一个对称中心是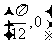
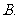 此函数的最小正周期为
此函数的最小正周期为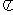 ,其图象的一个对称中心是
,其图象的一个对称中心是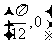
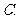 此函数的最小正周期为
此函数的最小正周期为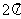 ,其图象的一个对称中心是
,其图象的一个对称中心是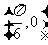
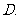 此函数的最小正周期为
此函数的最小正周期为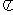 ,其图象的一个对称中心是
,其图象的一个对称中心是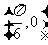
问题5.( 陕西)设函数
陕西)设函数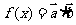 ,其中向量
,其中向量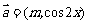 ,
,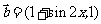 ,
,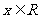 ,且
,且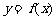 的图象经过点
的图象经过点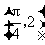 .(Ⅰ)求实数
.(Ⅰ)求实数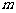 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数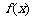 的最小值及此时
的最小值及此时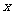 值的集合.
值的集合.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com