
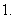 已知
已知 那么
那么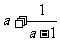 的最小值是
的最小值是 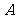
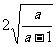
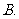
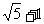
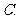
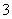
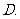
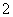
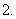 已知:
已知: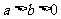 ,求证:
,求证: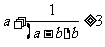
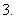 若
若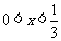 ,则
,则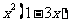 的最大值是
此时,
的最大值是
此时,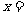
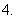 已知
已知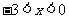 ,则
,则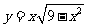 的最小值为
的最小值为 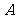
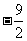
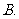
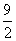
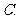
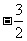
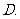
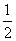
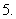 已知实数
已知实数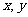 满足
满足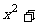
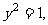 则
则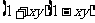 的最小值和最大值分别为
的最小值和最大值分别为
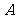
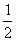 ,
,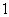
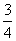 ,
,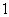
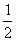 ,
,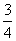
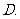
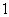 ,无最大值
,无最大值
 求
求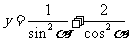
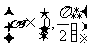 的最小值
的最小值
 当
当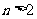 时,求证:
时,求证: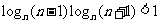 .
.
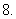 已知正数
已知正数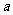 、
、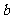 满足
满足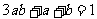 ,则
,则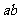 的最大值是
的最大值是
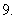 下列函数中,
下列函数中,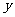 的最小值为
的最小值为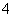 的是
的是
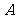
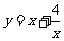
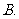
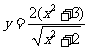
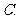
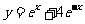
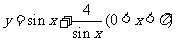
 若
若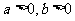 ,且
,且 ,则
,则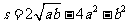 的最大值是
的最大值是
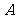
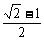
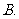
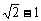
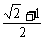
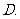
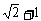
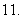 (
(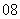 内江二中)已知
内江二中)已知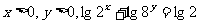 ,则
,则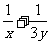 的最小值是
的最小值是
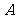
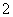
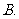
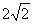
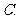
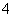
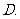
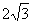
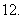 若
若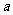 是正实数,
是正实数,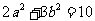 ,则
,则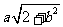 的最大值是
的最大值是
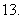 要使不等式
要使不等式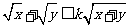 对所有正数
对所有正数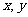 都成立,试问
都成立,试问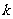 的最小值是
的最小值是
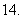 (
(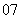 届高三西安市第一次质检)
届高三西安市第一次质检)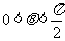 ,由不等式
,由不等式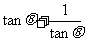 ≥
≥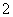 ,
,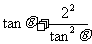
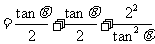 ≥
≥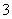 ,
,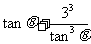
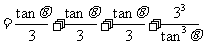 ≥
≥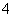 ,…,启发我们得到推广结论:
,…,启发我们得到推广结论:
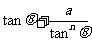 ≥
≥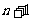
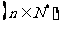 ,则
,则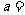
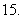 已知:
已知: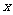 、
、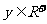 ,
,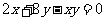 ,求
,求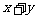 的最小值
的最小值
问题1.求下列函数的最值:
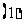
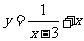
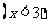 ;
;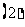
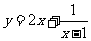
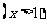 ;
;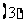
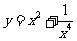
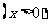 ;
;
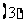
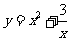
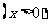 ;
;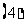
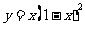
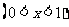 ;
;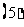
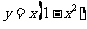
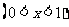
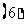
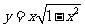
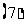 已知
已知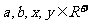 (
(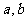 为常数),
为常数),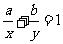 ,求
,求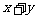 的最小值
的最小值
问题2.已知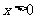 ,
,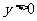 ,且
,且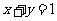 ,求
,求 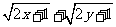 的最大值.
的最大值.
问题3.求最小值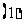
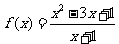
 ;
;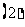
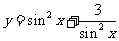
问题4. 设
设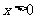 ,
,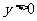 ,且
,且
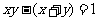 ,则
,则
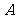
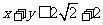
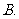
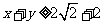
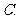
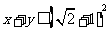
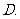
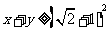
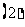 已知
已知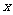 ≥
≥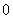 ,
,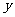 ≥
≥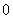 ,且
,且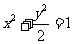 ,求证:
,求证: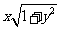 ≤
≤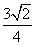
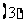 若
若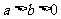 , 求
, 求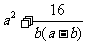 的最小值
的最小值
 常见构造条件的变换:加项变换,系数变换,平方变换,拆项变换,常量代换,三角代换等.
常见构造条件的变换:加项变换,系数变换,平方变换,拆项变换,常量代换,三角代换等. 当使用均值定理时等号不能成立时,应考虑函数的单调性(例如“对号”函数,导数法).
当使用均值定理时等号不能成立时,应考虑函数的单调性(例如“对号”函数,导数法).
 两个数的均值不等式:若
两个数的均值不等式:若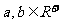 ,则
,则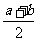 ≥
≥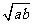 (等号仅当
(等号仅当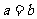 时成立)
时成立)
三个数的均值不等式:若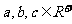 ,则
,则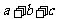 ≥
≥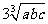 (等号仅当
(等号仅当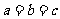 时成立)
时成立)
 几个重要的不等式:
几个重要的不等式:
① 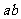 ≤
≤ ≤
≤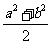 ②
②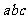 ≤
≤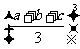 ;
;
③如果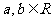 ,则
,则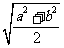 ≥
≥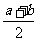 ≥
≥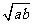 ≥
≥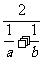
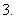 最值定理:当两个正数的和一定时,其乘积有最大值;当两个正数的乘积一定时,其和
最值定理:当两个正数的和一定时,其乘积有最大值;当两个正数的乘积一定时,其和
有最小值。
 (
( 全国Ⅰ)不等式
全国Ⅰ)不等式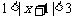 的解集为( ).
的解集为( ).
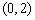
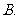
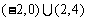
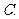
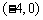
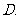
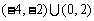
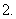 (
( 陕西)已知全集
陕西)已知全集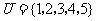 ,集合
,集合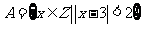 ,则
,则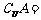
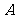
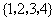
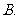
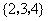
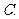
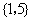
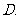
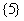
 (
( 安徽理) 设集合
安徽理) 设集合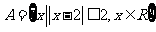 ,
,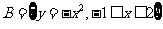 ,则
,则
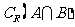 等于 ( )
等于 ( ) 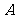
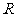
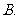
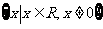
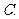
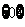
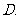
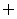
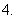 (
(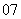 浙江)不等式
浙江)不等式 的解集是
.
的解集是
.
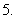 (
( 辽宁文,节选)设全集
辽宁文,节选)设全集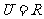 ,解关于
,解关于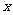 的不等式:
的不等式: 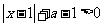
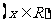
6. 已知不等式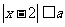
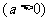 的解集为
的解集为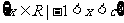 ,求
,求 的值
的值
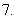 解关于
解关于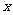 的不等式:①解关于
的不等式:①解关于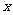 的不等式
的不等式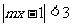 ;②
;②
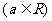
2. 解不等式: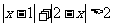
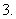 方程
方程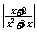
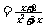 的解集为
,不等式
的解集为
,不等式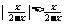 的解集是
的解集是
 (
( 湖北八校模拟)不等式
湖北八校模拟)不等式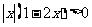 的解集是( )
的解集是( )
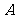
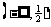
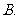
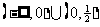
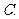
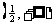
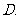
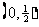
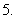 不等式
不等式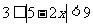 的解集是
的解集是
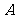
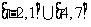
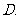
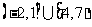
1. 不等式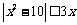 的解集为( )
的解集为( )
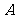
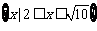
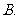
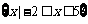
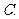
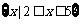
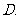
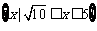
 解不等式:①
解不等式:① 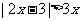 ;
②(
;
②(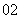 全国)
全国)
 (
( 新课程)若
新课程)若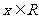 ,则
,则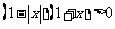 的解集是
的解集是
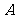
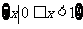
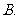
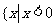 且
且
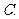
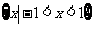
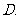
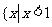 且
且
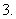
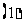 对任意实数
对任意实数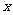 ,
,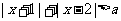 恒成立,则
恒成立,则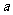 的取值范围是 ;
的取值范围是 ;
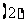 对任意实数
对任意实数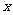 ,
,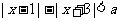 恒成立,则
恒成立,则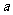 的取值范围是
的取值范围是
 若关于
若关于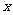 的不等式
的不等式 的解集不是空集,则
的解集不是空集,则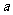 的取值范围是
的取值范围是
 解关于
解关于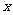 的不等式
的不等式 (
(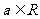 )
)
问题1:解下列不等式:
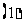
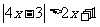 ;
;
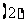
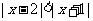 ;
;
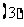
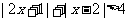 ;
;
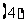
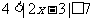
问题2.(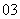 北京春)若不等式
北京春)若不等式 的解集为
的解集为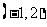 ,则实数
,则实数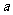 等于
等于
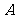
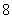
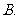
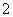
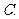

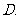

问题3. 设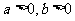 ,解关于
,解关于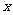 的不等式:
的不等式: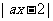 ≥
≥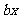 .
.
分析:本题是一个含有参数的不等式,解这类不等式时常要就参数的取值进行讨论。
问题4. 已知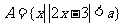 ,
,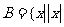 ≤
≤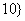 ,且
,且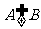 ,求实数
,求实数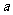 的范围
的范围
问题5. 在一条公路上,每隔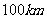 有个仓库(如下图),共有
有个仓库(如下图),共有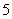 个仓库.一号仓库存有
个仓库.一号仓库存有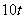 货物,二号仓库存
货物,二号仓库存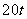 ,五号仓库存
,五号仓库存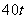 ,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输
,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输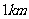 需要
需要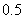 元运输费,那么最少要多少运费才行?
元运输费,那么最少要多少运费才行?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com